Numérique et Sciences Informatiques > Algorithmique : Structures de Données Avancées > Arbres Binaires > Parcours d'arbres (préfixe, infixe, suffixe)

Parcours d'arbres binaires : Préfixe, Infixe, Suffixe

Comprendre et implémenter les parcours d'arbres binaires : préfixe (préordre), infixe (inordre) et suffixe (postordre). Explications détaillées, exemples concrets et exercices pour maîtriser ces concepts essentiels en algorithmique.

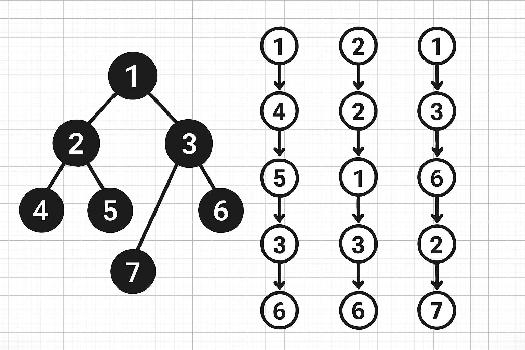
Introduction aux parcours d'arbres

Les parcours d'arbres binaires sont des méthodes systématiques pour visiter chaque nœud d'un arbre une seule fois. Il existe principalement trois types de parcours : le parcours préfixe (ou préordre), le parcours infixe (ou inordre) et le parcours suffixe (ou postordre). Chaque type de parcours a des applications spécifiques, et les comprendre est fondamental pour manipuler efficacement les arbres binaires. Ces parcours sont souvent implémentés de manière récursive, mais peuvent aussi être réalisés de manière itérative.

Parcours Préfixe (Préordre)

Le parcours préfixe (préordre) suit l'ordre suivant :

  1. Visiter la racine.
  2. Parcourir le sous-arbre gauche en préfixe.
  3. Parcourir le sous-arbre droit en préfixe.
En d'autres termes, on traite la racine *avant* de traiter ses enfants.

Exemple : Considérons l'arbre binaire suivant:

Arbre binaire


Le parcours préfixe de cet arbre serait : `F, B, A, D, C, E, G, I, H`.

Code (Python) :

def parcours_prefixe(racine):
  if racine:
    print(racine.valeur)
    parcours_prefixe(racine.gauche)
    parcours_prefixe(racine.droite)

Parcours Infixe (Inordre)

Le parcours infixe (inordre) suit l'ordre suivant :

  1. Parcourir le sous-arbre gauche en infixe.
  2. Visiter la racine.
  3. Parcourir le sous-arbre droit en infixe.
Ici, la racine est traitée *entre* ses enfants.

Exemple : En utilisant le même arbre que précédemment, le parcours infixe serait : `A, B, C, D, E, F, G, H, I`.

Code (Python) :

def parcours_infixe(racine):
  if racine:
    parcours_infixe(racine.gauche)
    print(racine.valeur)
    parcours_infixe(racine.droite)


Le parcours infixe est particulièrement utile pour les arbres binaires de recherche (BST), car il permet d'obtenir les nœuds dans l'ordre croissant.

Parcours Suffixe (Postordre)

Le parcours suffixe (postordre) suit l'ordre suivant :

  1. Parcourir le sous-arbre gauche en suffixe.
  2. Parcourir le sous-arbre droit en suffixe.
  3. Visiter la racine.
Dans ce cas, la racine est traitée *après* ses enfants.

Exemple : Toujours avec le même arbre, le parcours suffixe serait : `A, C, E, D, B, H, I, G, F`.

Code (Python) :

def parcours_suffixe(racine):
  if racine:
    parcours_suffixe(racine.gauche)
    parcours_suffixe(racine.droite)
    print(racine.valeur)

Applications des parcours d'arbres

Les parcours d'arbres ont diverses applications pratiques :

  • Parcours Préfixe : Utilisé pour la copie d'un arbre ou pour l'expression d'arbres syntaxiques (notation polonaise).
  • Parcours Infixe : Utilisé pour obtenir les éléments triés d'un arbre binaire de recherche (BST).
  • Parcours Suffixe : Utilisé pour la suppression d'un arbre (libération de la mémoire) ou pour l'évaluation d'expressions arithmétiques (notation polonaise inverse).

Complexité temporelle des parcours

Les trois types de parcours, préfixe, infixe et suffixe, ont la même complexité temporelle. Comme chaque noeud de l'arbre est visité une seule fois, la complexité est O(n), où 'n' est le nombre de noeuds dans l'arbre. C'est une complexité linéaire, ce qui signifie que le temps d'exécution augmente linéairement avec la taille de l'arbre.

Ce qu'il faut retenir

  • Les parcours d'arbres binaires permettent de visiter tous les nœuds d'un arbre d'une manière systématique.
  • Il existe trois principaux types de parcours : préfixe, infixe et suffixe, chacun ayant un ordre de visite différent.
  • Le parcours préfixe visite la racine avant les sous-arbres.
  • Le parcours infixe visite le sous-arbre gauche, puis la racine, puis le sous-arbre droit.
  • Le parcours suffixe visite les sous-arbres avant la racine.
  • Les parcours d'arbres ont des applications variées, allant de la copie d'arbres à l'évaluation d'expressions.
  • La complexité temporelle de ces parcours est O(n), où n est le nombre de nœuds de l'arbre.

← Opérations principales sur les listes chaînées : Insertion, Suppression et Recherche Piles et Files : Comprendre les principes LIFO et FIFO →

FAQ

  • Quelle est la différence entre un parcours préfixe et un parcours suffixe ?

    La principale différence réside dans l'ordre de visite de la racine. En parcours préfixe, la racine est visitée *avant* les sous-arbres, tandis qu'en parcours suffixe, la racine est visitée *après* les sous-arbres.
  • Pourquoi le parcours infixe est-il utile pour les arbres binaires de recherche (BST) ?

    Parce qu'il permet d'obtenir les nœuds dans l'ordre croissant. Un BST est structuré de telle sorte que tous les nœuds du sous-arbre gauche sont inférieurs à la racine, et tous les nœuds du sous-arbre droit sont supérieurs à la racine. Le parcours infixe exploite cette propriété.
  • Peut-on implémenter les parcours d'arbres de manière non récursive ?

    Oui, bien que la récursion soit une approche naturelle et élégante, les parcours d'arbres peuvent également être implémentés de manière itérative en utilisant une pile pour simuler la récursion.