Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Algèbre de Boole > Tables de vérité
Tables de Vérité : Le Guide Complet
Comprendre les tables de vérité en algèbre de Boole : définition, construction, exemples et applications. Un guide essentiel pour les élèves de lycée en Numérique et Sciences Informatiques.
Introduction aux Tables de Vérité
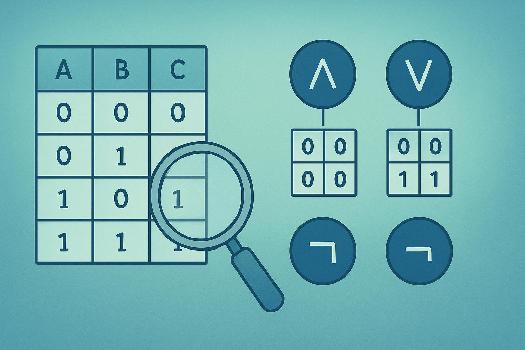
Les tables de vérité sont un outil fondamental en algèbre de Boole et en logique. Elles permettent de définir et d'évaluer les fonctions logiques. En termes simples, une table de vérité montre toutes les combinaisons possibles des entrées d'une fonction logique et la sortie correspondante pour chaque combinaison. C'est une représentation visuelle complète du comportement d'une expression booléenne.
Variables Booléennes et Opérateurs Logiques
Avant de construire une table de vérité, il est crucial de comprendre les variables booléennes et les opérateurs logiques de base :
- Variables Booléennes: Elles ne peuvent prendre que deux valeurs : Vrai (V) ou Faux (F), souvent représentées par 1 et 0 respectivement.
- Opérateur ET (AND): Noté souvent par un point (·) ou le symbole ∧. La sortie est Vrai uniquement si toutes les entrées sont Vrai.
- Opérateur OU (OR): Noté souvent par un plus (+) ou le symbole ∨. La sortie est Vrai si au moins une des entrées est Vrai.
- Opérateur NON (NOT): Noté souvent par une barre au-dessus de la variable (ex : Ā) ou le symbole ¬. Il inverse la valeur de l'entrée. Si l'entrée est Vrai, la sortie est Faux, et vice versa.
Construction d'une Table de Vérité
Voici les étapes pour construire une table de vérité :
- Identifier les variables d'entrée : Déterminez toutes les variables booléennes qui entrent dans l'expression logique.
- Énumérer toutes les combinaisons possibles : Pour n variables, il y a 2n combinaisons possibles. Listez-les toutes dans les colonnes d'entrée de la table. Généralement, on range les combinaisons de manière binaire.
- Évaluer l'expression logique pour chaque combinaison : Calculez la valeur de sortie de l'expression pour chaque ligne de la table en appliquant les opérateurs logiques appropriés.
- Compléter la table : Remplissez la colonne de sortie avec les valeurs calculées à l'étape précédente.
Exemple : Table de vérité pour l'expression A · B (A ET B)
| A | B | A · B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Exemples de Tables de Vérité
Exemple 1: Table de vérité pour A + B (A OU B)
| A | B | A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| A | ¬A |
|---|---|
| 0 | 1 |
| 1 | 0 |
| A | B | C | A · B | ¬C | (A · B) + ¬C |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Applications des Tables de Vérité
Les tables de vérité sont utilisées dans de nombreux domaines :
- Simplification des circuits logiques: Elles permettent de trouver des expressions logiques équivalentes plus simples.
- Conception de circuits numériques: Elles servent à définir le comportement des circuits et à vérifier leur bon fonctionnement.
- Programmation: Elles aident à comprendre et à optimiser les conditions logiques dans le code.
- Intelligence artificielle: Elles sont utilisées dans la représentation des connaissances et le raisonnement logique.
Ce qu'il faut retenir
- Une table de vérité représente toutes les combinaisons possibles des entrées d'une fonction logique et leurs sorties correspondantes.
- Les opérateurs logiques de base sont ET (AND), OU (OR) et NON (NOT).
- Pour n variables d'entrée, une table de vérité a 2n lignes.
- Les tables de vérité sont utilisées pour simplifier les circuits, concevoir des circuits numériques, optimiser le code et en IA.
- La construction d'une table de vérité comprend l'identification des variables, l'énumération des combinaisons, l'évaluation de l'expression et le remplissage de la table.
FAQ
-
Comment déterminer le nombre de lignes dans une table de vérité ?
Le nombre de lignes dans une table de vérité est égal à 2n, où n est le nombre de variables d'entrée. -
Quelle est la différence entre l'opérateur ET (AND) et l'opérateur OU (OR) ?
L'opérateur ET (AND) renvoie Vrai (1) uniquement si toutes ses entrées sont Vrai (1). L'opérateur OU (OR) renvoie Vrai (1) si au moins une de ses entrées est Vrai (1). -
Pourquoi les tables de vérité sont-elles importantes en informatique ?
Elles sont importantes car elles permettent de comprendre, concevoir et simplifier des circuits logiques, qui sont les fondations du matériel informatique. Elles aident également à la compréhension et à l'optimisation du code et à la représentation de la connaissance.
