Numérique et Sciences Informatiques > Numération et Bases > Opérations Binaires de Base > Soustraction binaire (notions)

La Soustraction Binaire : Principes de Base

Découvrez les fondements de la soustraction binaire, une opération essentielle en informatique. Ce guide détaillé, adapté aux lycéens, explique les règles, les retenues et les exemples concrets pour maîtriser la soustraction binaire sans difficulté.

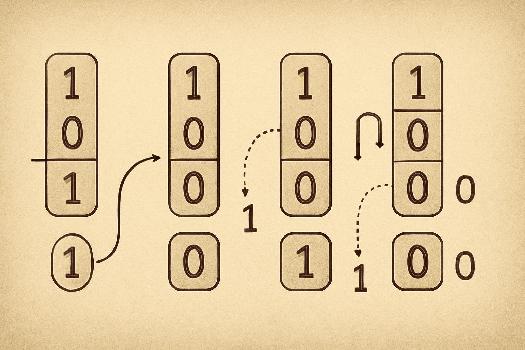
Introduction à la Soustraction Binaire

La soustraction binaire est une opération arithmétique fondamentale dans le système binaire, tout comme la soustraction décimale l'est dans le système décimal. Elle est cruciale en informatique car les ordinateurs fonctionnent en binaire (0 et 1). Comprendre la soustraction binaire est essentiel pour appréhender les opérations plus complexes effectuées par les processeurs.

Les Règles de Base de la Soustraction Binaire

La soustraction binaire repose sur quatre règles simples:

  • 0 - 0 = 0
  • 1 - 0 = 1
  • 1 - 1 = 0
  • 0 - 1 = 1 (avec une retenue de -1, que l'on "emprunte" au bit suivant)
La règle la plus importante à comprendre est la dernière : lorsque vous soustrayez 1 de 0, vous devez "emprunter" 1 de la colonne binaire suivante, ce qui est analogue à la retenue en soustraction décimale. L'emprunt transforme le 0 en 10 (qui vaut 2 en décimal), permettant ainsi de soustraire 1. Le résultat de cette soustraction est alors 1.

Exemples de Soustraction Binaire Simple

Voyons quelques exemples pour illustrer ces règles :

Opération Explication
1 - 0 = 1 Direct, pas de retenue.
1 - 1 = 0 Direct, pas de retenue.
0 - 0 = 0 Direct, pas de retenue.

Maintenant, un exemple avec retenue :

Opération Explication
10
- 1
-------
01		 On soustrait 1 de 0. On emprunte 1 à la colonne suivante (qui est un 1, devenant 0). Le 0 devient 10 (2 en décimal). 2 - 1 = 1. La colonne suivante est maintenant 0.

Note: En binaire, 10 représente 2 en décimal.

La Retenue (Emprunt) en Détail

L'emprunt, ou retenue négative, est l'étape la plus délicate de la soustraction binaire. Quand vous devez soustraire 1 d'un 0, vous devez emprunter 1 à la colonne binaire immédiatement à gauche. Cet emprunt transforme le 0 en 10 (qui équivaut à 2 en décimal) et le 1 de la colonne à gauche en 0. Si la colonne à gauche est également un 0, l'emprunt se propage jusqu'à ce qu'un 1 soit trouvé. Exemple plus complexe :

Opération Explication
100
- 011
-------
001		 1. On commence par la droite: 0 - 1. On emprunte 1 à la colonne suivante. 2. La colonne suivante est un 0, donc on doit emprunter à la colonne d'après. Le 1 devient 0 et transforme le second 0 en 10. 3. On emprunte 1 du 10 (qui devient 1) pour la première colonne, qui devient 10. Donc maintenant on a 10 - 1 = 1. Première colonne = 1. 4. On a 1 - 1 (car on avait emprunté 1 du 10). Cela fait 0. Deuxième colonne = 0. 5. La dernière colonne était un 1 qui est devenu 0 car on a emprunté deux fois. Donc 0 - 0 = 0. Troisième colonne = 0.

Soustraction binaire de nombres plus grands

Pour soustraire des nombres binaires plus grands, on applique les mêmes règles de base, colonne par colonne, en tenant compte des retenues. Exemple:

Opération Explication
1101
- 0110
-------
0111		 1. Première colonne (de droite) : 1 - 0 = 1 2. Deuxième colonne : 0 - 1 = 1 (avec une retenue de -1 de la colonne suivante) 3. Troisième colonne : 1 (moins la retenue) - 1 = 0 4. Quatrième colonne : 1 - 0 = 1 Résultat : 0111

Ce qu'il faut retenir

  • La soustraction binaire utilise uniquement les chiffres 0 et 1.
  • Les règles de base sont : 0 - 0 = 0, 1 - 0 = 1, 1 - 1 = 0, 0 - 1 = 1 (avec une retenue).
  • La retenue (ou emprunt) est nécessaire lorsque l'on soustrait 1 de 0.
  • La soustraction se fait colonne par colonne, de droite à gauche, en tenant compte des retenues.
  • Pour les opérations plus complexes, il est crucial de bien suivre l'ordre des opérations et de gérer correctement les retenues.

← La Base Hexadécimale : Un guide complet Opérations de Base en Binaire →

FAQ

  • Que se passe-t-il si j'ai besoin d'emprunter et que la colonne suivante est également un 0 ?

    Vous devez continuer à emprunter de la colonne suivante jusqu'à ce que vous trouviez un 1. Chaque 0 entre la colonne où vous empruntez et la colonne d'origine devient un 1, sauf la colonne d'où vous empruntez, qui devient un 0.
  • La soustraction binaire est-elle difficile à apprendre ?

    Au début, la notion de retenue peut sembler complexe, mais avec de la pratique, elle devient plus intuitive. Il est essentiel de bien comprendre les règles de base et de s'exercer avec des exemples variés.