Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Circuits Combinatoires Simples > Additionneur binaire (demi-additionneur, additionneur complet - principes)

Additionneurs Binaires : Demi-Additionneur et Additionneur Complet

Découvrez le fonctionnement des additionneurs binaires, composants essentiels de l'arithmétique des ordinateurs. Nous explorerons en détail le demi-additionneur et l'additionneur complet, en expliquant leurs principes, leurs tables de vérité et leurs applications.

Introduction à l'Addition Binaire

L'addition binaire est une opération fondamentale en informatique. Elle est à la base de toutes les opérations arithmétiques effectuées par les ordinateurs. Contrairement à l'addition décimale que nous utilisons quotidiennement, l'addition binaire ne manipule que deux chiffres : 0 et 1. Comprendre l'addition binaire est essentiel pour comprendre le fonctionnement des circuits logiques qui la mettent en œuvre.

Règles de l'Addition Binaire

L'addition binaire suit les règles suivantes:

  • 0 + 0 = 0
  • 0 + 1 = 1
  • 1 + 0 = 1
  • 1 + 1 = 10 (0 avec une retenue de 1)
La dernière règle est la plus importante : lorsque l'on additionne 1 et 1, le résultat est 0 et on génère une retenue de 1, que l'on doit ajouter à la colonne suivante.

Le Demi-Additionneur (Half Adder)

Le demi-additionneur est un circuit logique simple qui additionne deux bits (A et B) et produit deux sorties :

  • La Somme (S) : le résultat de l'addition des deux bits.
  • La Retenue (Cout) : la retenue générée si l'addition dépasse 1.

Table de Vérité du Demi-Additionneur:
ABSCout
0000
0110
1010
1101

Implémentation Logique:
  • Somme (S) = A XOR B
  • Retenue (Cout) = A AND B
Le demi-additionneur est limité car il ne prend pas en compte une éventuelle retenue provenant d'une addition précédente. C'est là qu'intervient l'additionneur complet.

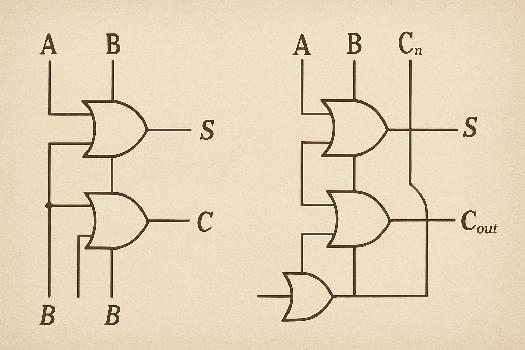
Le Circuit Logique du Demi-Additionneur

Un demi-additionneur peut être implémenté à l'aide de deux portes logiques de base: une porte XOR et une porte AND. La porte XOR produit la somme (S), tandis que la porte AND produit la retenue (Cout).

L'Additionneur Complet (Full Adder)

L'additionneur complet est un circuit logique plus complexe que le demi-additionneur. Il additionne trois bits :

  • A et B : les deux bits à additionner.
  • Cin : la retenue entrante (carry in) provenant d'une addition précédente.
Il produit également deux sorties :
  • La Somme (S) : le résultat de l'addition des trois bits.
  • La Retenue Sortante (Cout) : la retenue générée qui sera utilisée comme retenue entrante pour l'addition suivante.

Table de Vérité de l'Additionneur Complet:
ABCinSCout
00000
00110
01010
01101
10010
10101
11001
11111

Implémentation Logique:
L'additionneur complet peut être implémenté à l'aide de portes logiques XOR, AND et OR. Une façon courante de le concevoir est d'utiliser deux demi-additionneurs et une porte OR.
  • Somme (S) = A XOR B XOR Cin
  • Retenue (Cout) = (A AND B) OR (Cin AND (A XOR B))

Le Circuit Logique de l'Additionneur Complet

Un additionneur complet peut être construit en combinant deux demi-additionneurs. Le premier demi-additionneur additionne A et B, produisant une somme partielle et une retenue partielle. Le deuxième demi-additionneur additionne la somme partielle avec la retenue entrante (Cin). La retenue finale est obtenue en combinant les retenues des deux demi-additionneurs à l'aide d'une porte OR.

Utilisation des Additionneurs en Cascade

Pour additionner des nombres binaires de plusieurs bits, on utilise des additionneurs complets en cascade. La retenue sortante (Cout) d'un additionneur devient la retenue entrante (Cin) de l'additionneur suivant. Ainsi, on peut construire un additionneur 4 bits, 8 bits, 16 bits, etc.

Ce qu'il faut retenir

  • L'addition binaire est la base de l'arithmétique informatique.
  • Un demi-additionneur additionne deux bits et produit une somme et une retenue. Il ne tient pas compte d'une retenue entrante.
  • Un additionneur complet additionne trois bits (deux bits et une retenue entrante) et produit une somme et une retenue sortante.
  • Les additionneurs complets peuvent être utilisés en cascade pour additionner des nombres binaires de plusieurs bits.
  • Le demi-additionneur est composé d'une porte XOR (pour la somme) et d'une porte AND (pour la retenue).
  • L'additionneur complet peut être réalisé avec deux demi-additionneurs et une porte OR.

← Applications Pratiques des Portes Logiques →

FAQ

  • Quelle est la différence entre un demi-additionneur et un additionneur complet ?

    Le demi-additionneur additionne seulement deux bits, tandis que l'additionneur complet additionne trois bits (deux bits et une retenue entrante).
  • Pourquoi a-t-on besoin d'un additionneur complet ?

    L'additionneur complet est nécessaire pour additionner des nombres binaires de plusieurs bits, car il prend en compte les retenues générées lors des additions précédentes.
  • Comment additionner deux nombres binaires de 4 bits ?

    Vous pouvez utiliser quatre additionneurs complets en cascade. La retenue sortante de chaque additionneur est connectée à la retenue entrante de l'additionneur suivant.