Courbes de Bézier : La Magie des Lignes Vectorielles

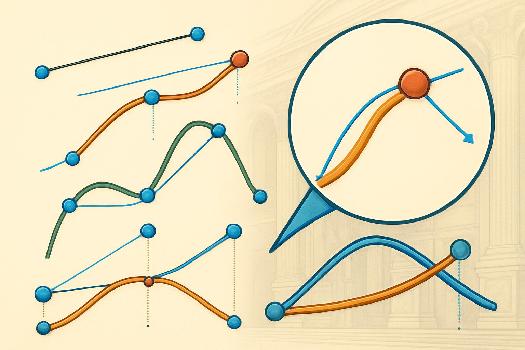
Introduction aux Courbes de Bézier

Les courbes de Bézier sont des courbes mathématiques utilisées dans les graphiques vectoriels pour représenter des courbes lisses. Elles sont définies par un ensemble de points de contrôle qui influencent la forme de la courbe. Contrairement aux segments de ligne droite, les courbes de Bézier permettent de créer des formes plus organiques et naturelles.

Elles sont omniprésentes dans les logiciels de design comme Adobe Illustrator, Inkscape et les outils de CAO (Conception Assistée par Ordinateur).

Définition Mathématique Simplifiée

Bien que la formule mathématique complète puisse être complexe, le concept de base est simple :

• Une courbe de Bézier est définie par un point de départ, un point d'arrivée, et un ou plusieurs points de contrôle.
• Les points de contrôle ne sont pas nécessairement situés sur la courbe elle-même. Ils agissent comme des aimants qui attirent la courbe.
• La position des points de contrôle détermine la forme et la courbure de la courbe.

Types de Courbes de Bézier

Il existe différents types de courbes de Bézier, en fonction du nombre de points de contrôle :

• Courbes de Bézier linéaires : Définies par deux points (départ et arrivée). C'est simplement un segment de ligne droite.
• Courbes de Bézier quadratiques : Définies par trois points (départ, contrôle, arrivée). Elles permettent de créer des courbes simples.
• Courbes de Bézier cubiques : Définies par quatre points (départ, contrôle 1, contrôle 2, arrivée). Ce sont les plus couramment utilisées car elles offrent une grande flexibilité pour créer des courbes complexes.

Utilisation des Points de Contrôle

Les points de contrôle sont cruciaux pour sculpter la forme de la courbe. Voici comment ils fonctionnent :

• En déplaçant un point de contrôle, vous modifiez la courbure de la courbe dans sa région.
• Plus un point de contrôle est éloigné du point de départ/arrivée, plus l'influence sur la courbure est forte.
• Les tangentes à la courbe au point de départ et au point d'arrivée passent par leurs points de contrôle respectifs.

Courbes de Bézier et Logiciels de Design

Les logiciels de design vectoriel utilisent des outils intuitifs pour manipuler les courbes de Bézier. Vous pouvez :

• Ajouter ou supprimer des points d'ancrage sur une courbe.
• Modifier la position des points de contrôle directement avec la souris.
• Ajuster l'angle et la longueur des tangentes des points de contrôle.
• Connecter des courbes de Bézier pour créer des formes complexes.

Ce qu'il faut retenir

• Les courbes de Bézier sont des courbes mathématiques définies par des points de contrôle.
• Elles sont utilisées pour créer des courbes lisses dans les graphiques vectoriels.
• Il existe différents types de courbes de Bézier (linéaires, quadratiques, cubiques).
• Les points de contrôle influencent la forme de la courbe.
• La manipulation des courbes de Bézier est essentielle pour le design vectoriel.