Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Algèbre de Boole > Tables de vérité

Simplification des expressions booléennes avec les tables de vérité : Méthode et exemples

Apprendre à simplifier des expressions booléennes complexes en utilisant les tables de vérité. Un guide essentiel pour les élèves de lycée en Numérique et Sciences Informatiques.

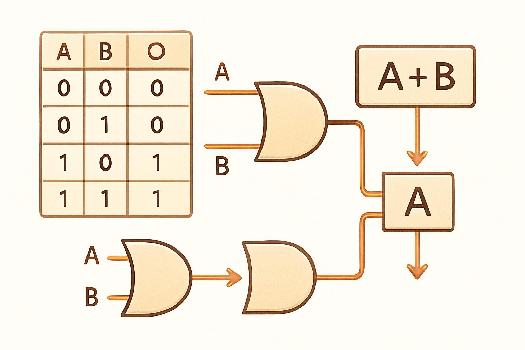
Introduction à la simplification

La simplification des expressions booléennes est un processus essentiel en algèbre de Boole. Il consiste à trouver une expression équivalente, mais plus simple, d'une expression donnée. Une expression simplifiée conduit à des circuits logiques plus simples, plus économiques et plus rapides. Les tables de vérité fournissent une méthode visuelle et systématique pour accomplir cette simplification.

Méthode de simplification avec les tables de vérité

La méthode générale pour simplifier une expression booléenne avec une table de vérité comprend les étapes suivantes:

  1. Construire la table de vérité : Créez une table de vérité pour l'expression booléenne que vous souhaitez simplifier. Assurez-vous d'inclure toutes les combinaisons possibles des variables d'entrée.
  2. Identifier les lignes de sortie '1' : Repérez toutes les lignes de la table de vérité où la sortie est égale à '1' (Vrai).
  3. Écrire le terme produit (minterme) pour chaque ligne '1' : Pour chaque ligne où la sortie est '1', écrivez un terme produit (minterme) qui correspond à cette combinaison d'entrées. Un minterme est une expression où chaque variable apparaît une seule fois, soit sous sa forme directe, soit sous sa forme complémentée (inversée). Par exemple, si A=0 et B=1, le minterme correspondant est ¬A · B.
  4. Combiner les mintermes : Combinez tous les mintermes identifiés à l'étape précédente en utilisant l'opérateur OU (+). Cette combinaison représente une forme normale disjonctive (FND) de l'expression.
  5. Simplifier la FND (si possible) : La FND obtenue peut souvent être simplifiée en utilisant les lois de l'algèbre de Boole (par exemple, les lois d'absorption, de De Morgan, etc.). Cette simplification peut conduire à une expression encore plus simple.

Exemple de simplification

Considérons l'expression booléenne : (A · B) + (A · ¬B). Nous allons utiliser une table de vérité pour simplifier cette expression.

  1. Construire la table de vérité :
    A B ¬B A · B A · ¬B (A · B) + (A · ¬B)
    0 0 1 0 0 0
    0 1 0 0 0 0
    1 0 1 0 1 1
    1 1 0 1 0 1
  2. Identifier les lignes de sortie '1' : Les lignes 3 et 4 ont une sortie de '1'.
  3. Écrire le minterme pour chaque ligne '1' :
    • Ligne 3 : A · ¬B
    • Ligne 4 : A · B
  4. Combiner les mintermes : (A · ¬B) + (A · B)
  5. Simplifier la FND : En utilisant la loi distributive, on peut factoriser A : A · (¬B + B). Comme (¬B + B) = 1, l'expression se simplifie à A · 1 = A.
Donc, l'expression (A · B) + (A · ¬B) est équivalente à A.

Un autre exemple

Simplifions l'expression: (A + B) · (A + ¬B).

  1. Construire la table de vérité:
    A B ¬B A + B A + ¬B (A + B) · (A + ¬B)
    0 0 1 0 1 0
    0 1 0 1 0 0
    1 0 1 1 1 1
    1 1 0 1 1 1
  2. Identifier les lignes de sortie '1': Les lignes 3 et 4 ont une sortie de '1'.
  3. Écrire le minterme pour chaque ligne '1': Dans ce cas, on considère les valeurs des entrées A et B.
    • Ligne 3: A · ¬B
    • Ligne 4: A · B
  4. Combiner les mintermes: (A · ¬B) + (A · B)
  5. Simplifier la FND: A · (¬B + B) = A · 1 = A
L'expression simplifiée est donc A.

Limitations et Considérations

Bien que les tables de vérité soient un outil puissant, elles peuvent devenir complexes pour les expressions avec un grand nombre de variables (plus de 4 ou 5). Dans ces cas, d'autres méthodes de simplification, comme les diagrammes de Karnaugh (K-maps) ou les algorithmes de minimisation, peuvent être plus efficaces. De plus, il est important de noter que la simplification avec les tables de vérité peut ne pas toujours donner la solution la plus simple possible, mais elle garantit de trouver une expression équivalente.

Ce qu'il faut retenir

  • La simplification des expressions booléennes est essentielle pour optimiser les circuits logiques.
  • Les tables de vérité fournissent une méthode visuelle et systématique pour la simplification.
  • La méthode consiste à construire la table de vérité, identifier les lignes de sortie '1', écrire les mintermes correspondants et combiner puis simplifier ces mintermes.
  • Les lois de l'algèbre de Boole sont utilisées pour simplifier la forme normale disjonctive (FND) obtenue.
  • Les tables de vérité peuvent devenir complexes pour les expressions avec un grand nombre de variables.

← Représentation Symbolique des Portes Logiques Fondamentales Tables de Vérité : Le Guide Complet →

FAQ

  • Pourquoi simplifier les expressions booléennes ?

    Simplifier les expressions booléennes conduit à des circuits logiques plus simples, moins coûteux et plus rapides, ce qui améliore l'efficacité globale des systèmes numériques.
  • Quand devrais-je utiliser les tables de vérité pour simplifier, plutôt que d'autres méthodes ?

    Les tables de vérité sont particulièrement utiles pour les expressions booléennes avec un petit nombre de variables (généralement 4 ou moins). Pour un plus grand nombre de variables, les diagrammes de Karnaugh ou d'autres techniques de minimisation peuvent être plus efficaces.
  • La simplification avec les tables de vérité garantit-elle la solution la plus simple possible ?

    Bien que la simplification avec les tables de vérité garantisse de trouver une expression équivalente, elle ne garantit pas toujours la solution la plus simple possible. Cependant, elle fournit une base solide pour d'autres simplifications manuelles.