Révisions Algorithmique : Complexité et Terminaison

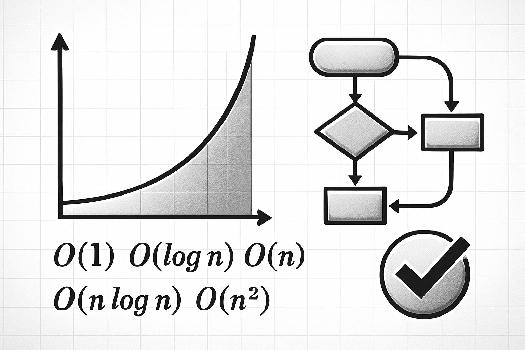
Introduction à la Complexité Algorithmique

La complexité algorithmique est une mesure de la quantité de ressources (temps et espace) nécessaires à un algorithme pour résoudre un problème. Elle est cruciale pour évaluer l'efficacité d'un algorithme, surtout lorsque l'on traite de grandes quantités de données.

Il existe deux types de complexité principaux :

• Complexité temporelle : Elle mesure le temps d'exécution de l'algorithme en fonction de la taille des données en entrée.
• Complexité spatiale : Elle mesure l'espace mémoire utilisé par l'algorithme en fonction de la taille des données en entrée.

On utilise souvent la notation de Landau (Grand O, O) pour exprimer la complexité asymptotique, c'est-à-dire le comportement de l'algorithme lorsque la taille des données tend vers l'infini.

Notation de Landau (Grand O)

La notation O(n) (prononcé « grand O de n ») décrit la limite supérieure de la croissance du temps d'exécution (ou de l'espace mémoire) d'un algorithme en fonction de la taille de l'entrée (n).

Quelques exemples courants :

• O(1) : Complexité constante. Le temps d'exécution ne dépend pas de la taille des données (par exemple, accéder à un élément dans un tableau à partir de son index).
• O(log n) : Complexité logarithmique. Le temps d'exécution augmente de manière logarithmique avec la taille des données (par exemple, recherche dichotomique dans un tableau trié).
• O(n) : Complexité linéaire. Le temps d'exécution augmente linéairement avec la taille des données (par exemple, parcourir un tableau).
• O(n log n) : Complexité quasi-linéaire (par exemple, tri fusion, tri rapide dans le meilleur des cas).
• O(n²) : Complexité quadratique. Le temps d'exécution augmente avec le carré de la taille des données (par exemple, tri à bulles, tri par insertion).
• O(2ⁿ) : Complexité exponentielle. Le temps d'exécution double à chaque augmentation de la taille des données (par exemple, recherche de toutes les combinaisons possibles).
• O(n!) : Complexité factorielle. Très coûteux, croît extrêmement vite avec la taille des données.

Il est essentiel de comprendre que la notation de Landau décrit le pire cas. Un algorithme peut avoir une complexité moyenne meilleure que sa complexité dans le pire des cas.

Exemples de Complexité Algorithmique

Considérons les exemples suivants :

• Recherche d'un élément dans un tableau non trié : Dans le pire des cas, il faut parcourir tout le tableau, donc la complexité est O(n).
• Recherche d'un élément dans un tableau trié (recherche dichotomique) : On divise l'espace de recherche par deux à chaque étape, donc la complexité est O(log n).
• Tri d'un tableau avec l'algorithme du tri à bulles : On compare chaque élément avec tous les autres, ce qui donne une complexité de O(n²).

Exemple de code Python (recherche linéaire):

def recherche_lineaire(tableau, element):
  for i in range(len(tableau)):
    if tableau[i] == element:
      return i  # Element trouvé à l'indice i
  return -1  # Element non trouvé

Exemple de code Python (recherche dichotomique):

def recherche_dichotomique(tableau, element):
  gauche = 0
  droite = len(tableau) - 1
  while gauche <= droite:
    milieu = (gauche + droite) // 2
    if tableau[milieu] == element:
      return milieu
    elif tableau[milieu] < element:
      gauche = milieu + 1
    else:
      droite = milieu - 1
  return -1

Terminaison des Algorithmes

La terminaison d'un algorithme signifie qu'il doit toujours s'arrêter après un nombre fini d'étapes, quelle que soit l'entrée. Un algorithme qui ne se termine jamais est inutile.

Pour prouver la terminaison d'un algorithme, on utilise souvent un variant de boucle. Un variant de boucle est une expression (généralement un entier) qui :

• Est toujours positive ou nulle.
• Diminue strictement à chaque itération de la boucle.

Si un variant de boucle existe, l'algorithme est garanti de se terminer car il ne peut pas diminuer indéfiniment tout en restant positif ou nul.

Exemples de Terminaison et Non-Terminaison

Exemple d'algorithme qui termine (recherche dichotomique) : Dans l'algorithme de recherche dichotomique, la taille de l'espace de recherche diminue de moitié à chaque itération. Le variant de boucle peut être la taille de l'espace de recherche (droite - gauche). Cette taille est toujours positive ou nulle et diminue à chaque itération. Donc, l'algorithme termine.

Exemple d'algorithme qui ne termine pas (boucle infinie) :

def boucle_infinie():
  i = 0
  while i < 10:
    # Pas d'incrémentation de i, la boucle ne se termine jamais
    print("Infini")

Dans cet exemple, la condition de la boucle (i < 10) est toujours vraie, car la valeur de i n'est jamais modifiée. La boucle s'exécute indéfiniment.

Exemple d'algorithme avec une terminaison conditionnelle:

def division_entiere(a, b):
  if b == 0:
    print("Erreur : division par zéro")
    return None  # Terminaison précoce si b est nul
  else:
    return a // b

Cet algorithme se termine toujours, soit en retournant le résultat de la division entière, soit en retournant None si la division par zéro est détectée.

Importance de la Complexité et de la Terminaison

La complexité et la terminaison sont des aspects fondamentaux de l'algorithmique. Comprendre la complexité permet de choisir l'algorithme le plus efficace pour un problème donné, en tenant compte des contraintes de temps et d'espace. S'assurer de la terminaison d'un algorithme garantit qu'il fournira toujours un résultat après un temps fini.

Ces concepts sont essentiels pour le développement de logiciels fiables et performants.

Ce qu'il faut retenir

• La complexité algorithmique mesure l'efficacité d'un algorithme en termes de temps et d'espace.
• La notation de Landau (Grand O) est utilisée pour exprimer la complexité asymptotique.
• O(1), O(log n), O(n), O(n log n), O(n²) sont des complexités courantes.
• La terminaison d'un algorithme signifie qu'il doit toujours s'arrêter.
• Un variant de boucle peut être utilisé pour prouver la terminaison d'un algorithme.