Numérique et Sciences Informatiques > Numération et Bases > Conversions de Bases > Décimal vers binaire et inversement

Conversion Décimal ↔ Binaire : Comprendre et Maîtriser

Apprenez à convertir facilement les nombres décimaux en binaires et vice-versa. Ce guide complet, avec des exemples détaillés, est parfait pour les élèves de lycée en NSI.

Introduction : Pourquoi le Binaire ?

En informatique, le système binaire est fondamental. Les ordinateurs utilisent des bits (0 et 1) pour représenter toutes les informations. Comprendre comment convertir entre le système décimal (base 10) et le système binaire (base 2) est donc crucial. Ce guide vous fournira les outils nécessaires pour maîtriser ces conversions.

De Décimal à Binaire : La Méthode de la Division Successive

La méthode la plus courante pour convertir un nombre décimal en binaire est la division successive par 2. Voici les étapes à suivre :

  1. Divisez le nombre décimal par 2. Notez le quotient et le reste.
  2. Divisez le quotient obtenu par 2. Notez à nouveau le quotient et le reste.
  3. Répétez l'étape 2 jusqu'à ce que le quotient soit égal à 0.
  4. Lisez les restes de bas en haut. La séquence des restes ainsi obtenue est la représentation binaire du nombre décimal.
Exemple : Conversion de 25 (décimal) en binaire
Division Quotient Reste
25 / 2 12 1
12 / 2 6 0
6 / 2 3 0
3 / 2 1 1
1 / 2 0 1
En lisant les restes de bas en haut, on obtient 11001. Donc, 25 (décimal) = 11001 (binaire).

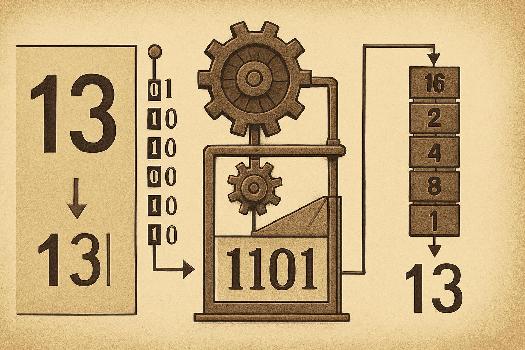
De Binaire à Décimal : La Méthode des Puissances de 2

Pour convertir un nombre binaire en décimal, on utilise la méthode des puissances de 2. Chaque position dans un nombre binaire représente une puissance de 2, en commençant par 20 à partir de la droite. Voici les étapes à suivre :

  1. Attribuez à chaque chiffre binaire une puissance de 2, en commençant par 20 pour le chiffre le plus à droite et en augmentant d'une puissance pour chaque chiffre vers la gauche.
  2. Multipliez chaque chiffre binaire par sa puissance de 2 correspondante.
  3. Additionnez les résultats de chaque multiplication. La somme obtenue est la représentation décimale du nombre binaire.
Exemple : Conversion de 10110 (binaire) en décimal
Chiffre Binaire Puissance de 2 Valeur
1 24 = 16 1 * 16 = 16
0 23 = 8 0 * 8 = 0
1 22 = 4 1 * 4 = 4
1 21 = 2 1 * 2 = 2
0 20 = 1 0 * 1 = 0
Somme : 16 + 0 + 4 + 2 + 0 = 22. Donc, 10110 (binaire) = 22 (décimal).

Cas Particuliers et Astuces

Conversion Rapide : Pour les petites valeurs, vous pouvez mémoriser les puissances de 2 (1, 2, 4, 8, 16, 32, 64, 128, ...). Cela peut accélérer la conversion de binaire à décimal.
Nombres Décimaux : La conversion de nombres décimaux (avec une virgule) en binaire est plus complexe et implique la multiplication successive de la partie fractionnaire par 2.

Applications en Informatique

La conversion décimal-binaire est utilisée dans divers domaines de l'informatique :

  • Adressage mémoire: Les adresses mémoire sont souvent représentées en binaire.
  • Représentation des données: Les caractères, les images et les sons sont tous convertis en binaire pour être stockés et traités par l'ordinateur.
  • Opérations logiques: Les opérations AND, OR, NOT, XOR sont effectuées sur des nombres binaires.

Ce qu'il faut retenir

  • Le système binaire est le langage des ordinateurs.
  • Conversion Décimal → Binaire: Division successive par 2 et lecture des restes de bas en haut.
  • Conversion Binaire → Décimal: Multiplication de chaque bit par sa puissance de 2 correspondante et sommation des résultats.
  • Les puissances de 2 sont cruciales pour la conversion binaire-décimal (1, 2, 4, 8, 16, 32, 64, 128...).
  • La conversion entre ces bases est essentielle pour comprendre le fonctionnement interne des ordinateurs.

← Conversion Binaire ↔ Hexadécimal : Guide Complet pour le Lycée Conversion Décimal-Hexadécimal et Réciproquement →

FAQ

  • Pourquoi les ordinateurs utilisent-ils le binaire ?

    Les ordinateurs utilisent le binaire car il est facile de représenter les états 'on' (1) et 'off' (0) avec des circuits électroniques. Cela rend le traitement de l'information simple et fiable.
  • La conversion décimale vers binaire est-elle toujours possible ?

    Oui, tout nombre décimal peut être converti en binaire. Cependant, la représentation binaire peut être infinie pour certains nombres décimaux fractionnaires.
  • Existe-t-il d'autres méthodes de conversion entre décimal et binaire ?

    Oui, il existe d'autres méthodes, mais la division successive et la méthode des puissances de 2 sont les plus courantes et les plus simples à comprendre.