Numérique et Sciences Informatiques > Logique Booléenne et Circuits Logiques (Bases) > Algèbre de Boole > Variables booléennes
Variables Booléennes et Table de Vérité
Approfondissez votre compréhension des variables booléennes à travers l'étude des tables de vérité. Apprenez comment ces tableaux permettent d'analyser et de simplifier des expressions booléennes complexes, un outil essentiel pour la conception de circuits logiques optimisés et la programmation efficace.
Introduction aux Tables de Vérité
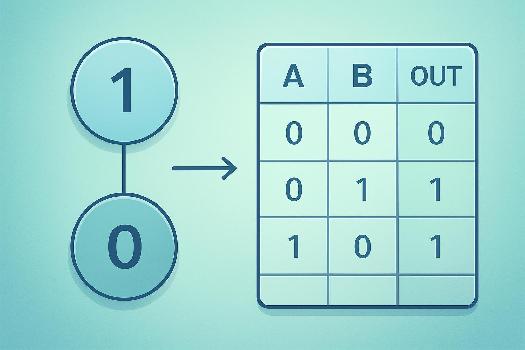
Une table de vérité est un outil fondamental en algèbre de Boole. C'est un tableau qui liste toutes les combinaisons possibles des valeurs d'entrée d'une ou plusieurs variables booléennes, ainsi que la valeur de sortie d'une expression logique pour chaque combinaison.
Les tables de vérité permettent de visualiser de manière exhaustive le comportement d'une fonction logique, de vérifier son bon fonctionnement et de simplifier des expressions booléennes.
Par exemple, si une expression booléenne dépend de deux variables (x et y), la table de vérité aura 22 = 4 lignes, une pour chaque combinaison de valeurs de x et y (00, 01, 10, 11).
Construction d'une Table de Vérité
Pour construire une table de vérité, suivez ces étapes :
- Identifiez les variables d'entrée: Déterminez quelles sont les variables booléennes qui composent l'expression logique.
- Créez les combinaisons d'entrée: Listez toutes les combinaisons possibles de valeurs (0 et 1) pour les variables d'entrée. Assurez-vous que toutes les combinaisons sont présentes.
- Évaluez l'expression logique: Pour chaque combinaison d'entrée, évaluez l'expression logique et notez la valeur de sortie (0 ou 1).
- Organisez les résultats: Présentez les résultats dans un tableau clair et lisible, avec les variables d'entrée et la sortie de l'expression logique.
Exemple: Construisons la table de vérité de l'expression x AND y:
| x | y | x AND y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Utilisation des Tables de Vérité pour la Simplification
Les tables de vérité peuvent être utilisées pour simplifier des expressions booléennes complexes. L'objectif est de trouver une expression plus simple qui produit la même table de vérité que l'expression originale.
Plusieurs techniques peuvent être utilisées, comme:
- Utilisation des identités booléennes: Appliquer les lois de l'algèbre de Boole (Commutativité, Associativité, Distributivité, etc.) pour simplifier l'expression.
- Méthode de Karnaugh: Utiliser un diagramme de Karnaugh pour identifier les regroupements de valeurs qui peuvent être simplifiés.
Exemple: Considérons l'expression (x AND y) OR (x AND NOT y). En construisant la table de vérité, on peut constater qu'elle est équivalente à l'expression plus simple x.
Applications des Tables de Vérité
Les tables de vérité ont de nombreuses applications dans différents domaines :
- Conception de circuits logiques: Elles permettent de spécifier le comportement d'un circuit et de vérifier sa conformité avec les exigences.
- Simplification d'expressions booléennes: Elles aident à réduire la complexité des expressions, ce qui peut conduire à des circuits plus simples et plus efficaces.
- Vérification de logiciels: Elles peuvent être utilisées pour tester des programmes et s'assurer qu'ils se comportent comme prévu.
- Intelligence artificielle: Elles sont utilisées dans les systèmes experts et les algorithmes de raisonnement logique.
Ce qu'il faut retenir
- Une table de vérité est un tableau qui liste toutes les combinaisons d'entrées et les sorties d'une expression booléenne.
- Elles sont utilisées pour visualiser et comprendre le comportement d'une fonction logique.
- Elles peuvent être utilisées pour simplifier des expressions booléennes complexes.
- Elles ont de nombreuses applications dans la conception de circuits, la vérification de logiciels et l'intelligence artificielle.
FAQ
-
Comment déterminer le nombre de lignes d'une table de vérité ?
Le nombre de lignes d'une table de vérité est égal à 2n, où n est le nombre de variables d'entrée. -
Pourquoi est-il important de simplifier les expressions booléennes ?
Simplifier les expressions booléennes permet de réduire la complexité des circuits logiques, ce qui peut conduire à des circuits plus petits, plus rapides et moins coûteux. -
Qu'est-ce qu'un diagramme de Karnaugh ?
Un diagramme de Karnaugh est une méthode graphique de simplification des expressions booléennes. Il permet de visualiser les regroupements de valeurs qui peuvent être simplifiés, en utilisant des règles spécifiques.
