Numérique et Sciences Informatiques > Algorithmique : Structures de Données Avancées > Listes Chaînées > Opérations principales (insertion, suppression, recherche)
Opérations principales sur les listes chaînées : Insertion, Suppression et Recherche
Découvrez les opérations fondamentales sur les listes chaînées : insertion, suppression et recherche. Ce guide détaillé, adapté aux élèves de lycée, explique chaque opération avec des exemples clairs et précis.
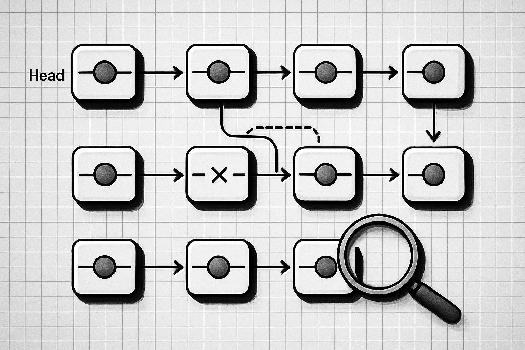
Introduction aux opérations sur les listes chaînées
Les listes chaînées sont des structures de données fondamentales en informatique, composées d'éléments appelés nœuds. Chaque nœud contient une donnée et un pointeur vers le nœud suivant dans la séquence. Contrairement aux tableaux, les listes chaînées ne nécessitent pas d'allocation contiguë de mémoire, ce qui les rend particulièrement utiles lorsque la taille des données est inconnue à l'avance ou lorsqu'il est nécessaire d'insérer ou de supprimer des éléments fréquemment.
Les opérations de base que l'on peut effectuer sur une liste chaînée sont l'insertion, la suppression et la recherche. Maîtriser ces opérations est essentiel pour manipuler efficacement les données stockées dans une liste chaînée.
Insertion d'un élément dans une liste chaînée
L'insertion consiste à ajouter un nouveau nœud à la liste. Il existe plusieurs façons d'insérer un nœud :
- Insertion en tête de liste : Le nouveau nœud devient le premier élément de la liste.
- Insertion en fin de liste : Le nouveau nœud est ajouté après le dernier nœud existant.
- Insertion à une position spécifique : Le nouveau nœud est inséré après un nœud existant, déterminé par une condition (par exemple, après un nœud contenant une valeur spécifique).
Exemple (insertion en tête) :
- Créer un nouveau nœud avec la donnée à insérer.
- Faire pointer le champ 'suivant' du nouveau nœud vers l'ancien premier nœud de la liste.
- Mettre à jour le pointeur de la tête de la liste pour qu'il pointe vers le nouveau nœud.
Exemple (insertion en position spécifique) : Imaginons que l'on souhaite insérer la valeur 30 après la valeur 20 dans la liste chaînée 10 -> 20 -> 40. On doit d'abord trouver le noeud contenant la valeur 20, créer un nouveau noeud contenant la valeur 30, faire pointer le 'suivant' du noeud 30 vers le noeud 40, et enfin faire pointer le 'suivant' du noeud 20 vers le noeud 30. La liste chaînée devient 10 -> 20 -> 30 -> 40.
Suppression d'un élément dans une liste chaînée
La suppression consiste à retirer un nœud de la liste. Comme pour l'insertion, il existe différentes méthodes de suppression :
- Suppression en tête de liste : Suppression du premier nœud de la liste.
- Suppression en fin de liste : Suppression du dernier nœud de la liste. (moins fréquent et plus coûteux en temps)
- Suppression d'un nœud spécifique : Suppression d'un nœud en fonction de sa valeur ou de sa position.
Exemple (suppression en tête) :
- Mettre à jour le pointeur de la tête de la liste pour qu'il pointe vers le deuxième nœud.
- Libérer la mémoire occupée par l'ancien premier nœud. (Important pour éviter les fuites de mémoire)
Exemple (suppression d'un nœud spécifique) : Si l'on veut supprimer le noeud contenant la valeur 20 dans la liste 10 -> 20 -> 30, on recherche le noeud précédent (contenant 10), on fait pointer le 'suivant' de ce noeud vers le noeud suivant celui que l'on veut supprimer (donc vers le noeud 30), et on libère la mémoire du noeud 20. La liste devient 10 -> 30.
Attention : La suppression nécessite de mettre à jour les pointeurs correctement pour éviter de casser la liste chaînée.
Recherche d'un élément dans une liste chaînée
La recherche consiste à trouver un nœud spécifique dans la liste, généralement en se basant sur sa valeur.
Algorithme :
- Parcourir la liste depuis la tête.
- Pour chaque nœud, comparer la valeur du nœud avec la valeur recherchée.
- Si la valeur est trouvée, retourner le nœud (ou un indicateur de succès).
- Si la fin de la liste est atteinte sans trouver la valeur, retourner un indicateur d'échec (par exemple, 'null').
Exemple : Pour rechercher la valeur 30 dans la liste 10 -> 20 -> 30 -> 40, on compare d'abord 10 avec 30 (pas de correspondance), puis 20 avec 30 (pas de correspondance), puis 30 avec 30 (correspondance ! On a trouvé le noeud).
Complexité : La recherche dans une liste chaînée est généralement de complexité O(n), car dans le pire des cas (l'élément recherché n'est pas dans la liste ou est en fin de liste), il faut parcourir tous les nœuds.
Complexité temporelle des opérations
Comprendre la complexité temporelle des opérations sur les listes chaînées est crucial pour optimiser votre code et choisir la structure de données la plus appropriée pour un problème donné. Voici un aperçu de la complexité temporelle des opérations principales :
| Opération | Complexité temporelle | Explication |
|---|---|---|
| Insertion en tête | O(1) | L'insertion en tête ne nécessite que la mise à jour du pointeur de tête et du nouveau nœud, ce qui prend un temps constant. |
| Insertion en fin | O(n) | Dans une liste simplement chaînée, l'insertion en fin nécessite de parcourir toute la liste pour trouver le dernier nœud, ce qui prend un temps proportionnel à la taille de la liste. Si on conserve un pointeur vers le dernier élément, l'insertion en fin devient O(1). |
| Insertion à une position spécifique | O(n) | Dans le pire des cas, il faut parcourir toute la liste pour trouver la position d'insertion, ce qui prend un temps proportionnel à la taille de la liste. |
| Suppression en tête | O(1) | La suppression en tête ne nécessite que la mise à jour du pointeur de tête, ce qui prend un temps constant. |
| Suppression en fin | O(n) | La suppression en fin nécessite de parcourir toute la liste pour trouver l'avant-dernier nœud, ce qui prend un temps proportionnel à la taille de la liste. |
| Suppression d'un nœud spécifique | O(n) | Dans le pire des cas, il faut parcourir toute la liste pour trouver le nœud à supprimer, ce qui prend un temps proportionnel à la taille de la liste. |
| Recherche | O(n) | Dans le pire des cas, il faut parcourir toute la liste pour trouver l'élément recherché (ou constater qu'il n'existe pas), ce qui prend un temps proportionnel à la taille de la liste. |
Important : La complexité temporelle est un facteur clé dans le choix d'une structure de données. Pour des opérations fréquentes d'insertion/suppression en tête, une liste chaînée est très efficace (O(1)). Cependant, pour des recherches fréquentes, un tableau (si trié) ou une table de hachage peuvent être plus performants.
Ce qu'il faut retenir
- Listes chaînées : Structures de données composées de nœuds, chacun contenant une donnée et un pointeur vers le nœud suivant.
- Insertion : Ajout d'un nouveau nœud à la liste (en tête, en fin ou à une position spécifique).
- Suppression : Retrait d'un nœud de la liste (en tête, en fin ou un nœud spécifique).
- Recherche : Trouver un nœud spécifique dans la liste en fonction de sa valeur.
- Complexité temporelle : L'insertion/suppression en tête est O(1), mais la recherche et l'insertion/suppression en fin (sans pointeur vers le dernier élément) sont O(n).
FAQ
-
Quelle est la principale différence entre un tableau et une liste chaînée ?
Les tableaux nécessitent une allocation contiguë de mémoire, tandis que les listes chaînées allouent de la mémoire pour chaque nœud individuellement. Cela rend les listes chaînées plus flexibles pour l'insertion et la suppression, mais potentiellement moins efficaces pour l'accès aléatoire. -
Pourquoi est-il important de libérer la mémoire après avoir supprimé un nœud dans une liste chaînée ?
Ne pas libérer la mémoire entraîne des fuites de mémoire, ce qui peut ralentir le programme et éventuellement le faire planter. Libérer la mémoire permet de la rendre disponible pour une utilisation ultérieure. -
Comment optimiser l'insertion en fin de liste dans une liste chaînée?
En conservant un pointeur vers le dernier élément de la liste, l'insertion en fin devient une opération O(1) car vous n'avez plus besoin de parcourir toute la liste pour trouver le dernier noeud.
