Numérique et Sciences Informatiques > Numération et Bases > Systèmes de Numération > Base décimale

Base Décimale : Représentation des Entiers Relatifs

Explorez comment la base décimale est utilisée pour représenter les nombres entiers relatifs (positifs et négatifs). Découvrez les conventions et méthodes pour exprimer ces nombres dans le système décimal.

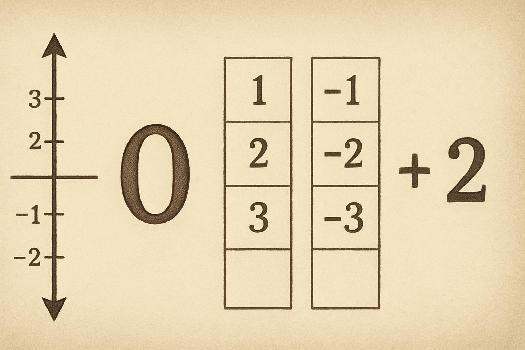
Introduction aux Entiers Relatifs

Les entiers relatifs comprennent les nombres entiers positifs (1, 2, 3, ...), les nombres entiers négatifs (-1, -2, -3, ...) et zéro (0). La base décimale est utilisée pour représenter tous ces nombres. La distinction entre nombres positifs et négatifs est généralement faite en utilisant le signe '+' pour les positifs (bien que souvent omis) et le signe '-' pour les négatifs.

Représentation des Entiers Positifs

Les entiers positifs sont représentés directement en base décimale comme nous l'avons vu précédemment. Par exemple, le nombre 25 est représenté simplement comme '25'. Le signe '+' est souvent implicite.

Représentation des Entiers Négatifs

Les entiers négatifs sont représentés en base décimale en utilisant le signe moins '-' devant le nombre. Par exemple, moins cinq est représenté par '-5'. Il est important de noter que le signe '-' fait partie intégrante du nombre et indique sa nature négative.

L'Importance du Zéro

Le zéro (0) est un élément crucial dans le système de numération décimal et dans la représentation des entiers relatifs. Il représente l'absence de quantité et sert de point de référence entre les nombres positifs et négatifs. Il n'est ni positif ni négatif.

Opérations Arithmétiques avec les Entiers Relatifs

Effectuer des opérations arithmétiques avec des entiers relatifs nécessite de tenir compte des règles de signes:

Addition:

  • Si les deux nombres ont le même signe, on additionne leurs valeurs absolues et on conserve le signe commun.
  • Si les deux nombres ont des signes différents, on soustrait la plus petite valeur absolue de la plus grande et on conserve le signe du nombre ayant la plus grande valeur absolue.

Soustraction: Soustraire un nombre revient à additionner son opposé.

Multiplication et Division:
  • Si les deux nombres ont le même signe, le résultat est positif.
  • Si les deux nombres ont des signes différents, le résultat est négatif.

Ce qu'il faut retenir

  • Les entiers relatifs comprennent les nombres positifs, négatifs et zéro.
  • Les entiers positifs sont représentés directement en base décimale.
  • Les entiers négatifs sont précédés du signe '-'.
  • Le zéro est le point de référence entre les nombres positifs et négatifs.
  • Les opérations arithmétiques avec les entiers relatifs nécessitent de tenir compte des règles de signes.

← Addition Binaire : Principes et Applications Comprendre la Base Binaire →

FAQ

  • Comment comparer deux entiers relatifs en base décimale ?

    Pour comparer deux entiers relatifs, on peut utiliser la droite numérique. Les nombres les plus à droite sont les plus grands. Un nombre positif est toujours plus grand qu'un nombre négatif. Entre deux nombres négatifs, celui qui a la plus petite valeur absolue est le plus grand (par exemple, -2 est plus grand que -5).
  • Existe-t-il d'autres façons de représenter les nombres négatifs en informatique ?

    Oui, en informatique, il existe d'autres méthodes pour représenter les nombres négatifs, comme le complément à deux. Cette représentation est utilisée pour simplifier les opérations arithmétiques et faciliter leur implémentation matérielle.