SVT > Génétique des Populations > Fréquences Alléliques et Génotypiques > Loi de Hardy-Weinberg (notions)

Exercices d'application : Loi de Hardy-Weinberg

Mise en pratique de la loi de Hardy-Weinberg à travers des exercices variés pour consolider la compréhension des concepts et des calculs.

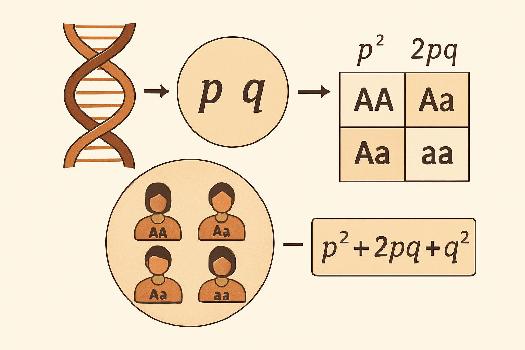
Exercice 1 : Fréquences alléliques et génotypiques

Dans une population de papillons, la couleur des ailes est déterminée par un seul gène avec deux allèles : un allèle dominant N pour la couleur noire et un allèle récessif n pour la couleur blanche. Dans cette population, 36% des papillons sont blancs.

  1. Quelle est la fréquence de l'allèle récessif n ?
  2. Quelle est la fréquence de l'allèle dominant N ?
  3. Quelles sont les fréquences génotypiques attendues pour NN, Nn et nn si la population est en équilibre de Hardy-Weinberg ?

Solution :

  1. La fréquence du génotype nn est de 0.36. Donc, q2 = 0.36, ce qui implique que q = √0.36 = 0.6. La fréquence de l'allèle n est donc 0.6.
  2. Puisque p + q = 1, p = 1 - q = 1 - 0.6 = 0.4. La fréquence de l'allèle N est donc 0.4.
  3. Les fréquences génotypiques attendues sont :
    - NN : p2 = 0.42 = 0.16
    - Nn : 2pq = 2 * 0.4 * 0.6 = 0.48
    - nn : q2 = 0.62 = 0.36

Exercice 2 : Test d'équilibre de Hardy-Weinberg

Dans une population de 500 individus, on observe les génotypes suivants pour un certain gène :

  • AA : 245
  • Aa : 210
  • aa : 45
  1. Calculez les fréquences génotypiques observées.
  2. Calculez les fréquences alléliques A et a.
  3. En utilisant la loi de Hardy-Weinberg, calculez les fréquences génotypiques attendues.
  4. Comparez les fréquences génotypiques observées et attendues. La population est-elle en équilibre de Hardy-Weinberg ? (Une analyse statistique plus poussée, comme un test du Chi-deux, serait nécessaire pour une conclusion formelle, mais une comparaison visuelle permet déjà de donner une indication).

Solution :

  1. Les fréquences génotypiques observées sont :
    - AA : 245 / 500 = 0.49
    - Aa : 210 / 500 = 0.42
    - aa : 45 / 500 = 0.09
  2. Pour calculer les fréquences alléliques:
    - La fréquence de l'allèle A (p) est calculée comme suit: p = (2 * nombre de AA + nombre de Aa) / (2 * nombre total d'individus) = (2*245 + 210) / (2 * 500) = 700/1000 = 0.7
    - La fréquence de l'allèle a (q) est calculée comme suit: q = (2 * nombre de aa + nombre de Aa) / (2 * nombre total d'individus) = (2*45 + 210) / (2 * 500) = 300/1000 = 0.3
    On peut aussi calculer q comme q = 1-p = 1 - 0.7 = 0.3
  3. Les fréquences génotypiques attendues sous l'équilibre de Hardy-Weinberg sont:
    - AA : p2 = 0.72 = 0.49
    - Aa : 2pq = 2 * 0.7 * 0.3 = 0.42
    - aa : q2 = 0.32 = 0.09
  4. En comparant les fréquences observées et attendues, on constate qu'elles sont identiques. Bien qu'un test statistique soit préférable, on peut suggérer que la population est probablement en équilibre de Hardy-Weinberg pour ce gène.

Exercice 3 : Allèles liés au sexe

(Cet exercice est plus avancé et peut être omis lors d'une première introduction à la loi de Hardy-Weinberg). Chez l'humain, la capacité à distinguer les couleurs rouge et vert est liée au chromosome X. Supposons que dans une population, 8% des hommes sont daltoniens (incapables de distinguer le rouge et le vert). Le daltonisme est causé par un allèle récessif d sur le chromosome X.

  1. Quelle est la fréquence de l'allèle d dans cette population ?
  2. Quelles sont les fréquences génotypiques attendues pour les femmes : XDXD, XDXd, et XdXd ?
  3. Quel pourcentage de femmes devraient être daltoniennes ?

Solution :

  1. Puisque les hommes n'ont qu'un seul chromosome X, la fréquence de l'allèle d (q) est égale à la fréquence des hommes daltoniens. Donc q = 0.08.
  2. Si q = 0.08, alors p (fréquence de l'allèle XD) = 1 - q = 1 - 0.08 = 0.92. Les fréquences génotypiques attendues pour les femmes sont :
    - XDXD : p2 = 0.922 = 0.8464
    - XDXd : 2pq = 2 * 0.92 * 0.08 = 0.1472
    - XdXd : q2 = 0.082 = 0.0064
  3. Seules les femmes XdXd sont daltoniennes. Le pourcentage attendu de femmes daltoniennes est donc de 0.64%.

Ce qu'il faut retenir

  • La loi de Hardy-Weinberg permet de calculer les fréquences alléliques et génotypiques attendues dans une population en équilibre.
  • En comparant les fréquences observées et attendues, on peut évaluer si une population est en équilibre et identifier les forces évolutives qui agissent sur elle.
  • Les exercices d'application permettent de consolider la compréhension des concepts et de maîtriser les calculs associés à la loi de Hardy-Weinberg.
  • Il est important de bien identifier les allèles dominants et récessifs et de comprendre comment la loi s'applique aux gènes autosomiques et liés au sexe.

← Exercices d'application : Facteurs de variation des fréquences alléliques Facteurs de variation des fréquences alléliques et génotypiques →

FAQ

  • Est-ce que toutes les populations naturelles sont en équilibre de Hardy-Weinberg ?

    Non, la plupart des populations naturelles ne sont pas en équilibre de Hardy-Weinberg car les conditions nécessaires (absence de mutations, absence de flux génétique, accouplement aléatoire, absence de sélection naturelle, population de grande taille) sont rarement toutes respectées. Cependant, la loi de Hardy-Weinberg reste un outil précieux pour comprendre l'évolution.
  • Comment puis-je savoir si une population dévie de l'équilibre de Hardy-Weinberg ?

    En comparant les fréquences génotypiques observées avec les fréquences génotypiques attendues sous l'équilibre de Hardy-Weinberg. Si les fréquences sont significativement différentes, cela suggère que la population dévie de l'équilibre. Un test statistique, comme le test du Chi-deux, peut être utilisé pour évaluer la signification de cette différence.