Suites Numériques : Exercices Corrigés pour le Bac

Définition d'une Suite Numérique

Une suite numérique est une fonction définie sur l'ensemble des entiers naturels (ou une partie de cet ensemble) à valeurs réelles. On la note généralement (u_n), où u_n représente le terme général de la suite. Il est crucial de comprendre que n est un entier et que la suite est une liste ordonnée de nombres réels. Une suite peut être définie de plusieurs manières :

• Explicitement: u_n = f(n), où f est une fonction. Par exemple, u_n = n² + 1.
• Par récurrence: On donne le premier terme (ou les premiers termes) et une relation qui permet de calculer u_n+1 en fonction de u_n (ou des termes précédents). Par exemple, u₀ = 2 et u_n+1 = 3u_n - 1.

Calcul des Premiers Termes

L'étape initiale pour comprendre une suite est souvent de calculer ses premiers termes. Cela peut aider à identifier un motif ou une tendance.
Exemple 1 (Suite explicite): u_n = 2n - 3. Alors :

• u₀ = 2(0) - 3 = -3
• u₁ = 2(1) - 3 = -1
• u₂ = 2(2) - 3 = 1
• u₃ = 2(3) - 3 = 3

• u₀ = 1 (donné)
• u₁ = u₀ + 2 = 1 + 2 = 3
• u₂ = u₁ + 2 = 3 + 2 = 5
• u₃ = u₂ + 2 = 5 + 2 = 7

Limites de Suites

La limite d'une suite (u_n) est la valeur vers laquelle les termes de la suite se rapprochent quand n tend vers l'infini.

• Si (u_n) tend vers un nombre réel L, on dit que la suite converge vers L. On note lim_n→∞ u_n = L.
• Si (u_n) tend vers +∞ ou -∞, on dit que la suite diverge.
• Si (u_n) n'a pas de limite (par exemple, elle oscille entre deux valeurs), on dit aussi que la suite diverge.

• Théorèmes de comparaison: Si u_n ≤ v_n et lim_n→∞ v_n = L, alors lim_n→∞ u_n ≤ L.
• Théorème des gendarmes: Si u_n ≤ v_n ≤ w_n et lim_n→∞ u_n = lim_n→∞ w_n = L, alors lim_n→∞ v_n = L.
• Opérations sur les limites: La limite d'une somme, d'un produit, d'un quotient de suites est la somme, le produit, le quotient des limites (sous réserve que les opérations soient définies).

Suites Arithmétiques

Une suite (u_n) est arithmétique s'il existe un nombre réel r (appelé raison) tel que, pour tout n, u_n+1 = u_n + r.

• Le terme général d'une suite arithmétique est donné par : u_n = u₀ + nr.
• La somme des n premiers termes d'une suite arithmétique est donnée par : S_n = n(u₀ + u_n-1)/2 = n(2u₀ + (n-1)r)/2.

Suites Géométriques

Une suite (u_n) est géométrique s'il existe un nombre réel q (appelé raison) tel que, pour tout n, u_n+1 = qu_n.

• Le terme général d'une suite géométrique est donné par : u_n = u₀qⁿ.
• La somme des n premiers termes d'une suite géométrique est donnée par : S_n = u₀(1 - qⁿ)/(1 - q) (si q ≠ 1). Si q = 1, S_n = nu₀.

Exercice Corrigé 1 : Suite Définie par Récurrence

Énoncé: Soit (u_n) la suite définie par u₀ = 1 et u_n+1 = (1/2)u_n + 3.

1. Montrer que la suite (v_n) définie par v_n = u_n - 6 est une suite géométrique. Préciser sa raison et son premier terme.
2. Exprimer v_n en fonction de n. En déduire l'expression de u_n en fonction de n.
3. Calculer la limite de la suite (u_n).

1. v_n+1 = u_n+1 - 6 = (1/2)u_n + 3 - 6 = (1/2)u_n - 3 = (1/2)(u_n - 6) = (1/2)v_n. Donc (v_n) est une suite géométrique de raison q = 1/2 et de premier terme v₀ = u₀ - 6 = 1 - 6 = -5.
2. v_n = v₀ * qⁿ = -5 * (1/2)ⁿ. Donc u_n = v_n + 6 = -5 * (1/2)ⁿ + 6.
3. lim_n→∞ (1/2)ⁿ = 0 car |1/2| < 1. Donc lim_n→∞ u_n = -5 * 0 + 6 = 6.

Exercice Corrigé 2 : Suite Arithmético-Géométrique

Énoncé: On considère la suite (u_n) définie par u₀ = 2 et u_n+1 = 0.8u_n + 0.6 pour tout entier naturel n.

1. Calculer u₁, u₂ et u₃.
2. On pose v_n = u_n - 3. Montrer que la suite (v_n) est une suite géométrique. Préciser sa raison et son premier terme.
3. Exprimer v_n en fonction de n. En déduire l'expression de u_n en fonction de n.
4. Déterminer la limite de la suite (u_n).

1. u₁ = 0.8 * 2 + 0.6 = 2.2; u₂ = 0.8 * 2.2 + 0.6 = 2.36; u₃ = 0.8 * 2.36 + 0.6 = 2.488.
2. v_n+1 = u_n+1 - 3 = 0.8u_n + 0.6 - 3 = 0.8u_n - 2.4 = 0.8(u_n - 3) = 0.8v_n. Donc (v_n) est une suite géométrique de raison q = 0.8 et de premier terme v₀ = u₀ - 3 = 2 - 3 = -1.
3. v_n = v₀ * qⁿ = -1 * (0.8)ⁿ. Donc u_n = v_n + 3 = -(0.8)ⁿ + 3.
4. lim_n→∞ (0.8)ⁿ = 0 car |0.8| < 1. Donc lim_n→∞ u_n = -0 + 3 = 3.

Ce qu'il faut retenir

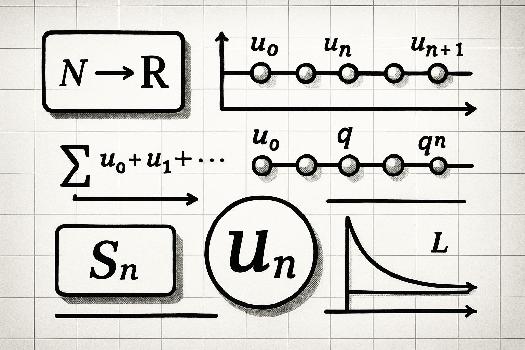
• Définition d'une suite: Une fonction de N vers R.
• Suites arithmétiques: u_n+1 = u_n + r. Terme général: u_n = u₀ + nr. Somme des n premiers termes: S_n = n(u₀ + u_n-1)/2.
• Suites géométriques: u_n+1 = qu_n. Terme général: u_n = u₀qⁿ. Somme des n premiers termes: S_n = u₀(1 - qⁿ)/(1 - q).
• Limites de suites: Convergence vers une valeur finie. Divergence vers l'infini ou absence de limite.
• Techniques de calcul de limites: Théorèmes de comparaison, théorème des gendarmes, opérations sur les limites.
• Formes indéterminées: Savoir les identifier et les lever (factorisation, simplification, etc.).