Bac S Maths 2018 - Probabilités : Corrigé détaillé et expliqué

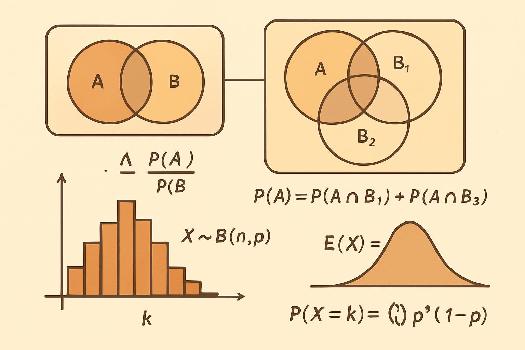
Question 1 : Probabilités conditionnelles

Calculons la probabilité de l'événement A sachant B, notée P(A|B). Rappelons la formule : P(A|B) = P(A inter B) / P(B). Dans notre cas, cela signifie la probabilité qu'une pièce soit défectueuse sachant qu'elle a été fabriquée par la machine 1. Nous devons identifier P(D inter M1) et P(M1) dans l'énoncé. L'énoncé nous indique que 60% des pièces sont fabriquées par la machine 1, donc P(M1) = 0.6. Il indique également que 5% des pièces fabriquées par la machine 1 sont défectueuses, donc P(D|M1) = 0.05. Nous cherchons P(D inter M1). Nous savons que P(D|M1) = P(D inter M1) / P(M1), donc P(D inter M1) = P(D|M1) * P(M1) = 0.05 * 0.6 = 0.03. Donc la probabilité qu'une pièce soit défectueuse et provienne de la machine 1 est de 0.03.

Question 2 : Probabilité totale

Pour calculer la probabilité qu'une pièce soit défectueuse, nous devons considérer les deux machines. Utilisons la formule des probabilités totales : P(D) = P(D inter M1) + P(D inter M2). Nous avons déjà calculé P(D inter M1) = 0.03. Calculons P(D inter M2). L'énoncé nous indique que 40% des pièces sont fabriquées par la machine 2, donc P(M2) = 0.4. Il indique également que 2% des pièces fabriquées par la machine 2 sont défectueuses, donc P(D|M2) = 0.02. Donc P(D inter M2) = P(D|M2) * P(M2) = 0.02 * 0.4 = 0.008. Par conséquent, P(D) = 0.03 + 0.008 = 0.038. La probabilité qu'une pièce soit défectueuse est de 0.038.

Question 3 : Variable aléatoire

Soit X la variable aléatoire représentant le nombre de pièces défectueuses dans un échantillon de 10 pièces. On effectue 10 tirages indépendants, et à chaque tirage, la probabilité qu'une pièce soit défectueuse est de 0.038 (calculée précédemment). Donc X suit une loi binomiale de paramètres n = 10 et p = 0.038, notée X ~ B(10, 0.038). Nous cherchons la probabilité qu'il y ait au moins une pièce défectueuse, c'est-à-dire P(X >= 1). Il est plus simple de calculer l'événement complémentaire : P(X >= 1) = 1 - P(X = 0). La probabilité d'avoir 0 pièce défectueuse est donnée par la formule de la loi binomiale : P(X = 0) = (10 choose 0) * (0.038)^0 * (1 - 0.038)^10 = 1 * 1 * (0.962)^10 ≈ 0.684. Donc P(X >= 1) = 1 - 0.684 = 0.316. La probabilité d'avoir au moins une pièce défectueuse dans un échantillon de 10 pièces est d'environ 0.316.

Question 4 : Espérance mathématique

L'espérance mathématique d'une variable aléatoire binomiale X ~ B(n, p) est donnée par la formule E(X) = n * p. Dans notre cas, n = 10 et p = 0.038. Donc E(X) = 10 * 0.038 = 0.38. Cela signifie qu'en moyenne, on s'attend à trouver 0.38 pièces défectueuses dans un échantillon de 10 pièces.

Ce qu'il faut retenir

• Probabilités conditionnelles : P(A|B) = P(A ∩ B) / P(B)
• Probabilité totale : P(A) = P(A ∩ B1) + P(A ∩ B2) + ... + P(A ∩ Bn) si les événements B1, B2, ..., Bn forment une partition de l'univers.
• Loi binomiale : X ~ B(n, p) si X compte le nombre de succès dans n épreuves indépendantes, chacune ayant une probabilité de succès p.
• Formule de la loi binomiale : P(X = k) = (n choose k) * p^k * (1 - p)^(n-k)
• Espérance mathématique d'une loi binomiale : E(X) = n * p