Préparation au Baccalauréat > Annales et Corrigés : Mathématiques > Exercices et Problèmes par Thème > Probabilités et Statistiques

Probabilités Conditionnelles et Indépendance : Exercices et Corrigés

Comprenez et maîtrisez les probabilités conditionnelles et l'indépendance d'événements avec des exercices corrigés, des exemples clairs et une explication pas à pas. Préparation optimale pour le Baccalauréat.

Définition et Notation

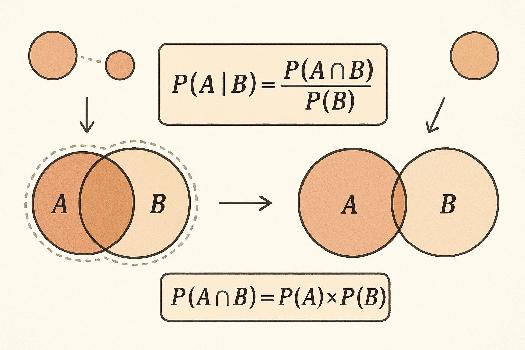
La probabilité conditionnelle d'un événement A sachant que l'événement B est réalisé est notée P(A|B) et se lit 'probabilité de A sachant B'. Elle représente la probabilité que A se produise si on sait déjà que B s'est produit. Mathématiquement, si P(B) ≠ 0, alors P(A|B) = P(A ∩ B) / P(B). Il est crucial de bien identifier quel événement est la condition (ce qui est déjà arrivé).

Exemple Concret

Imaginons un sac contenant des billes rouges et bleues. On tire une bille au hasard.

  • A: La bille est rouge.
  • B: La bille a un numéro pair.
Alors, P(A|B) est la probabilité que la bille soit rouge sachant qu'elle a un numéro pair. Pour la calculer, on ne considère que les billes avec un numéro pair et on regarde quelle proportion d'entre elles sont rouges.

Calcul de P(A|B)

Pour calculer P(A|B), vous avez besoin de deux informations:

  • P(A ∩ B): La probabilité que A et B se produisent ensemble (bille rouge et numéro pair).
  • P(B): La probabilité que B se produise (bille avec un numéro pair).
Divisez P(A ∩ B) par P(B) pour obtenir P(A|B). Attention : L'ordre est important ! P(A|B) est différent de P(B|A).

Indépendance d'Événements

Deux événements A et B sont indépendants si la réalisation de l'un n'influence pas la probabilité de l'autre. Mathématiquement, A et B sont indépendants si et seulement si P(A|B) = P(A) (si P(B) ≠ 0) ou, de manière équivalente, si P(A ∩ B) = P(A) * P(B). Exemple: Lancer une pièce deux fois. Le résultat du premier lancer (pile ou face) n'affecte pas le résultat du deuxième lancer. Les deux lancers sont des événements indépendants.

Exercice 1: Pioche dans un jeu de 32 cartes

On tire une carte au hasard dans un jeu de 32 cartes. On considère les événements suivants :

  • C : « La carte tirée est un cœur »
  • R : « La carte tirée est un roi »
  1. Calculer P(C) et P(R).
  2. Calculer P(C ∩ R).
  3. Les événements C et R sont-ils indépendants ? Justifier.
Correction :
  1. P(C) = 8/32 = 1/4 ; P(R) = 4/32 = 1/8
  2. P(C ∩ R) = 1/32 (il y a un seul roi de cœur)
  3. P(C) * P(R) = (1/4) * (1/8) = 1/32 = P(C ∩ R). Donc les événements C et R sont indépendants.

Exercice 2: Lancer de dé

On lance un dé à six faces non truqué. On considère les événements suivants :

  • A : « On obtient un nombre pair »
  • B : « On obtient un nombre supérieur ou égal à 3 »
  1. Calculer P(A) et P(B).
  2. Calculer P(A ∩ B).
  3. Calculer P(A|B).
  4. Les événements A et B sont-ils indépendants ? Justifier.
Correction :
  1. P(A) = 3/6 = 1/2 ; P(B) = 4/6 = 2/3
  2. P(A ∩ B) = 2/6 = 1/3 (on obtient 4 ou 6)
  3. P(A|B) = P(A ∩ B) / P(B) = (1/3) / (2/3) = 1/2
  4. P(A|B) = P(A) donc les événements A et B sont indépendants.

Ce qu'il faut retenir

  • Probabilité Conditionnelle: P(A|B) = P(A ∩ B) / P(B) (si P(B) ≠ 0). Représente la probabilité de A sachant que B est réalisé.
  • Indépendance: A et B sont indépendants si P(A|B) = P(A) (si P(B) ≠ 0) ou si P(A ∩ B) = P(A) * P(B). La réalisation de l'un n'influence pas la probabilité de l'autre.
  • Bien identifier: L'événement conditionnant (ce qu'on sait déjà) est crucial. P(A|B) ≠ P(B|A) en général.
  • Formules clés: Savoir appliquer les formules pour calculer les probabilités conditionnelles et vérifier l'indépendance.

← Optimiser Votre Préparation en Mathématiques: Méthodes et Astuces Essentielles Résolution d'équations du second degré →

FAQ

  • Quelle est la différence entre P(A|B) et P(B|A) ?

    P(A|B) est la probabilité que l'événement A se produise sachant que l'événement B s'est déjà produit. P(B|A) est la probabilité que l'événement B se produise sachant que l'événement A s'est déjà produit. En général, ils sont différents. Il est crucial de bien identifier quel événement est la condition.
  • Comment puis-je savoir si deux événements sont indépendants ?

    Deux événements A et B sont indépendants si P(A|B) = P(A) (si P(B) ≠ 0) ou de manière équivalente si P(A ∩ B) = P(A) * P(B). Si l'une de ces conditions est vérifiée, alors les événements sont indépendants.