Bac S Maths 2019 - Suites Numériques : Corrigé détaillé et expliqué

Question 1 : Calcul des premiers termes

Calculons les premiers termes de la suite (u_n) définie par u₀ = 2 et u_n+1 = (1/3)u_n + 2.

Pour trouver u₁, on remplace n par 0 dans la relation de récurrence : u₁ = (1/3)u₀ + 2 = (1/3)*2 + 2 = 2/3 + 6/3 = 8/3.

Pour trouver u₂, on remplace n par 1 : u₂ = (1/3)u₁ + 2 = (1/3)*(8/3) + 2 = 8/9 + 18/9 = 26/9.

Question 2 : Suite géométrique

Soit la suite (v_n) définie par v_n = u_n - 3. Montrons que (v_n) est une suite géométrique. Pour cela, calculons v_n+1 en fonction de v_n.

v_n+1 = u_n+1 - 3 = (1/3)u_n + 2 - 3 = (1/3)u_n - 1.

On veut exprimer ceci en fonction de v_n = u_n - 3, donc u_n = v_n + 3. Remplaçons u_n dans l'expression de v_n+1 : v_n+1 = (1/3)(v_n + 3) - 1 = (1/3)v_n + 1 - 1 = (1/3)v_n.

Ainsi, v_n+1 = (1/3)v_n. Ceci prouve que (v_n) est une suite géométrique de raison q = 1/3. Son premier terme est v₀ = u₀ - 3 = 2 - 3 = -1.

Question 3 : Expression de u_n en fonction de n

Puisque (v_n) est une suite géométrique de premier terme v₀ = -1 et de raison q = 1/3, son terme général est donné par v_n = v₀ * qⁿ = -1 * (1/3)ⁿ = -(1/3)ⁿ.

On sait que v_n = u_n - 3, donc u_n = v_n + 3 = 3 - (1/3)ⁿ.

Question 4 : Limite de la suite (u_n)

Calculons la limite de la suite (u_n) quand n tend vers l'infini. u_n = 3 - (1/3)ⁿ.

Quand n tend vers l'infini, (1/3)ⁿ tend vers 0, car 1/3 est compris entre -1 et 1. Donc lim (1/3)ⁿ = 0 quand n -> ∞.

Par conséquent, lim u_n = 3 - 0 = 3 quand n -> ∞. La suite (u_n) converge vers 3.

Ce qu'il faut retenir

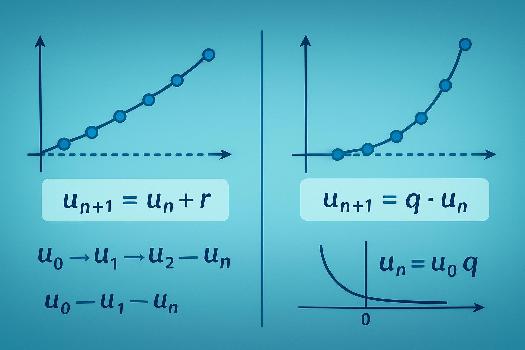
• Suite arithmétique : u_n+1 = u_n + r, où r est la raison.
• Suite géométrique : u_n+1 = q * u_n, où q est la raison.
• Terme général d'une suite géométrique : u_n = u₀ * qⁿ
• Limite d'une suite géométrique : Si |q| < 1, alors lim qⁿ = 0 quand n -> ∞.
• Convergence d'une suite : Une suite (u_n) converge vers L si lim u_n = L quand n -> ∞.