Préparation au Baccalauréat > Annales et Corrigés : Mathématiques > Exercices et Problèmes par Thème > Géométrie

Exercices Corrigés de Géométrie Analytique pour le Bac

Explorez des exercices corrigés de géométrie analytique, spécialement conçus pour la préparation au Baccalauréat. Apprenez à maîtriser les concepts clés tels que les vecteurs, les droites, les cercles et les transformations géométriques à travers des exemples détaillés et des explications claires.

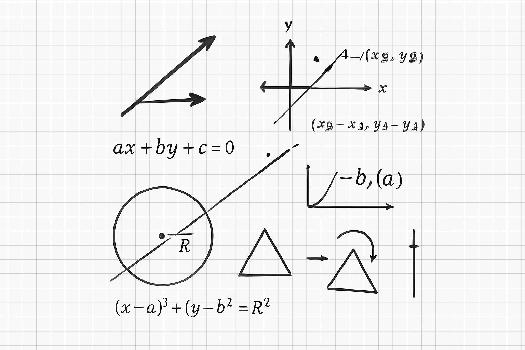
Vecteurs et Repérage dans le Plan

Définition d'un vecteur: Un vecteur est défini par sa direction, son sens et sa norme. Il est souvent représenté par une flèche reliant deux points A et B, noté . Sa norme est la longueur du segment AB, notée ||||.
Coordonnées d'un vecteur dans un repère orthonormé: Si A(xA, yA) et B(xB, yB), alors a pour coordonnées (xB - xA, yB - yA).
Opérations sur les vecteurs:
  • Addition: (xu, yu) + (xv, yv) = (xu + xv, yu + yv)
  • Multiplication par un scalaire: k * (xu, yu) = (k * xu, k * yu)
Exemple: Soient A(1, 2) et B(4, 6). a pour coordonnées (4 - 1, 6 - 2) = (3, 4). La norme de est |||| = = 5.

Équations de Droites

Équation cartésienne: Une droite (D) peut être définie par une équation de la forme ax + by + c = 0, où a, b et c sont des nombres réels et (a, b) ≠ (0, 0).
Vecteur directeur: Un vecteur directeur d'une droite d'équation ax + by + c = 0 a pour coordonnées (-b, a).
Vecteur normal: Un vecteur normal d'une droite d'équation ax + by + c = 0 a pour coordonnées (a, b).
Équation réduite: Si b ≠ 0, on peut écrire l'équation sous la forme y = mx + p, où m est la pente (coefficient directeur) et p est l'ordonnée à l'origine.
Droites parallèles et perpendiculaires:
  • Deux droites sont parallèles si et seulement si elles ont le même coefficient directeur.
  • Deux droites sont perpendiculaires si et seulement si le produit de leurs coefficients directeurs est égal à -1.
Exemple: La droite d'équation 2x + 3y - 6 = 0 a pour vecteur directeur (-3, 2) et pour vecteur normal (2, 3). Son coefficient directeur est -2/3 et son ordonnée à l'origine est 2.

Cercles

Équation d'un cercle: Un cercle de centre Ω(a, b) et de rayon R a pour équation (x - a)² + (y - b)² = R².
Exemple: Le cercle de centre (2, -1) et de rayon 3 a pour équation (x - 2)² + (y + 1)² = 9.
Intersection d'une droite et d'un cercle: Pour trouver les points d'intersection entre une droite et un cercle, on résout le système d'équations formé par l'équation de la droite et celle du cercle. Le nombre de solutions indique le nombre de points d'intersection (0, 1 ou 2).

Transformations Géométriques

Translation: Une translation de vecteur transforme un point M(x, y) en un point M'(x', y') tel que = . Si a pour coordonnées (a, b), alors x' = x + a et y' = y + b.
Rotation: Une rotation de centre O et d'angle θ transforme un point M en un point M' tel que OM = OM' et l'angle () = θ. Les formules de rotation sont x' = x cos θ - y sin θ et y' = x sin θ + y cos θ.
Symétrie axiale: Une symétrie axiale par rapport à une droite (D) transforme un point M en un point M' tel que (D) est la médiatrice du segment [MM'].
Symétrie centrale: Une symétrie centrale par rapport à un point O transforme un point M en un point M' tel que O est le milieu du segment [MM'].

Ce qu'il faut retenir

  • Un vecteur est défini par sa direction, son sens et sa norme.
  • Les coordonnées d'un vecteur sont (xB - xA, yB - yA).
  • L'équation cartésienne d'une droite est ax + by + c = 0.
  • Le vecteur directeur d'une droite d'équation ax + by + c = 0 est (-b, a).
  • L'équation d'un cercle de centre (a, b) et de rayon R est (x - a)² + (y - b)² = R².
  • Les transformations géométriques incluent les translations, rotations, symétries axiales et symétries centrales.

← Bac S Maths 2019 - Suites Numériques : Corrigé détaillé et expliqué Exercices Corrigés de Géométrie dans l'Espace pour le Bac →

FAQ

  • Comment déterminer si deux droites sont parallèles ?

    Deux droites sont parallèles si et seulement si elles ont le même coefficient directeur (même pente) dans leur équation réduite (y = mx + p). Si elles sont données sous forme cartésienne (ax + by + c = 0), elles sont parallèles si le rapport de leurs coefficients est le même (a1/a2 = b1/b2).
  • Comment trouver le point d'intersection entre une droite et un cercle ?

    Pour trouver le point d'intersection, il faut résoudre le système d'équations formé par l'équation de la droite et celle du cercle. Cela implique généralement de substituer l'équation de la droite dans celle du cercle, ou vice versa, et de résoudre l'équation résultante. Le nombre de solutions indique le nombre de points d'intersection.