Préparation au Baccalauréat > Annales et Corrigés : Mathématiques > Exercices et Problèmes par Thème > Algèbre

Résolution d'équations du second degré

Méthode complète et détaillée pour résoudre les équations du second degré : calcul du discriminant, identification des solutions réelles et complexes. Avec exemples concrets.

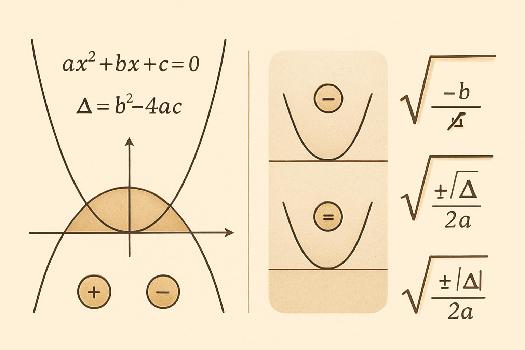
Définition et Forme Générale

Une équation du second degré, aussi appelée équation quadratique, est une équation polynomiale dont le degré le plus élevé est 2. Sa forme générale est donnée par: ax2 + bx + c = 0, où a, b et c sont des coefficients réels (ou complexes), et a ≠ 0. Si a était égal à 0, l'équation deviendrait une équation du premier degré.

Le Discriminant (Δ)

La clé pour résoudre une équation du second degré réside dans le calcul du discriminant, noté Δ (delta). Le discriminant est défini par la formule : Δ = b2 - 4ac. La valeur du discriminant détermine le nombre et la nature des solutions de l'équation.

Interprétation du Discriminant

  • Δ > 0 : L'équation possède deux solutions réelles distinctes. Cela signifie que la parabole représentative de l'équation coupe l'axe des abscisses en deux points différents.
  • Δ = 0 : L'équation possède une solution réelle double (ou deux solutions réelles identiques). La parabole est tangente à l'axe des abscisses.
  • Δ < 0 : L'équation ne possède pas de solutions réelles. Elle possède deux solutions complexes conjuguées. La parabole ne coupe pas l'axe des abscisses.

Formule des Solutions

Lorsque Δ ≥ 0, les solutions réelles de l'équation sont données par la formule: x1,2 = (-b ± √Δ) / 2a. Si Δ < 0, les solutions complexes sont données par: x1,2 = (-b ± i√|Δ|) / 2a, où i est l'unité imaginaire (i2 = -1).

Exemple 1 : Δ > 0

Résolvons l'équation : x2 - 5x + 6 = 0. Ici, a = 1, b = -5, et c = 6. Calculons le discriminant : Δ = (-5)2 - 4 * 1 * 6 = 25 - 24 = 1. Puisque Δ > 0, il y a deux solutions réelles : x1 = (5 + √1) / 2 = 3 et x2 = (5 - √1) / 2 = 2.

Exemple 2 : Δ = 0

Résolvons l'équation : x2 - 4x + 4 = 0. Ici, a = 1, b = -4, et c = 4. Calculons le discriminant : Δ = (-4)2 - 4 * 1 * 4 = 16 - 16 = 0. Puisque Δ = 0, il y a une solution réelle double : x = (4 ± √0) / 2 = 2.

Exemple 3 : Δ < 0

Résolvons l'équation : x2 + 2x + 5 = 0. Ici, a = 1, b = 2, et c = 5. Calculons le discriminant : Δ = (2)2 - 4 * 1 * 5 = 4 - 20 = -16. Puisque Δ < 0, il y a deux solutions complexes conjuguées : x1,2 = (-2 ± i√16) / 2 = -1 ± 2i.

Ce qu'il faut retenir

  • La forme générale d'une équation du second degré est ax2 + bx + c = 0.
  • Le discriminant (Δ) est calculé par la formule Δ = b2 - 4ac.
  • Si Δ > 0 : deux solutions réelles distinctes.
  • Si Δ = 0 : une solution réelle double.
  • Si Δ < 0 : deux solutions complexes conjuguées.
  • Les solutions sont données par x1,2 = (-b ± √Δ) / 2a (pour Δ ≥ 0) ou x1,2 = (-b ± i√|Δ|) / 2a (pour Δ < 0).

← Probabilités Conditionnelles et Indépendance : Exercices et Corrigés Stratégies Efficaces pour Réussir l'Épreuve de Mathématiques au Baccalauréat →

FAQ

  • Comment identifier a, b et c dans une équation du second degré ?

    Identifiez le coefficient devant x2 (c'est a), le coefficient devant x (c'est b), et la constante (c'est c). Par exemple, dans l'équation 2x2 - 3x + 1 = 0, a = 2, b = -3, et c = 1.
  • Que signifie 'solutions complexes conjuguées' ?

    Des solutions complexes conjuguées sont des nombres complexes de la forme a + bi et a - bi, où a et b sont des nombres réels et i est l'unité imaginaire (√-1).