Préparation au Baccalauréat > Annales et Corrigés : Mathématiques > Exercices et Problèmes par Thème > Algèbre

Suites Numériques : Définitions et Propriétés

Introduction aux suites numériques : définitions, types (arithmétiques, géométriques), limites et convergence. Exemples et exercices corrigés.

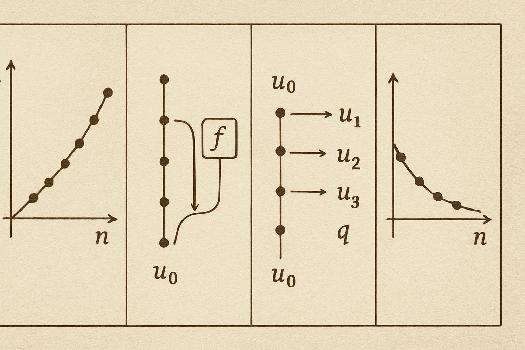
Définition d'une Suite Numérique

Une suite numérique est une fonction définie sur l'ensemble des entiers naturels (ℕ) ou une partie de ℕ, et qui prend ses valeurs dans l'ensemble des nombres réels (ℝ) ou complexes (ℂ). On la note généralement (un), où n est l'indice de la suite. Chaque un est un terme de la suite.

Modes de Définition d'une Suite

Il existe principalement deux manières de définir une suite :

  • Par une formule explicite : un = f(n), où f est une fonction de n. Par exemple, un = n2 + 1.
  • Par récurrence : On définit le premier terme (ou les premiers termes) et une relation de récurrence qui exprime un+1 en fonction de un (ou des termes précédents). Par exemple, u0 = 1 et un+1 = 2un + 1.

Suites Arithmétiques

Une suite est dite arithmétique si la différence entre deux termes consécutifs est constante. Cette constante est appelée la raison de la suite, souvent notée r. Ainsi, un+1 = un + r. Le terme général d'une suite arithmétique est donné par : un = u0 + n * r (si la suite commence à l'indice 0) ou un = u1 + (n-1) * r (si la suite commence à l'indice 1).

Suites Géométriques

Une suite est dite géométrique si le rapport entre deux termes consécutifs est constant. Cette constante est appelée la raison de la suite, souvent notée q. Ainsi, un+1 = q * un. Le terme général d'une suite géométrique est donné par : un = u0 * qn (si la suite commence à l'indice 0) ou un = u1 * qn-1 (si la suite commence à l'indice 1).

Convergence et Limites

On dit qu'une suite (un) converge vers une limite L si, pour tout ε > 0 (aussi petit soit-il), il existe un entier N tel que pour tout n > N, |un - L| < ε. Cela signifie que les termes de la suite se rapprochent de plus en plus de la valeur L lorsque n tend vers l'infini. On note alors lim (n→∞) un = L. Si une suite ne converge pas, elle diverge. Une suite peut diverger vers l'infini (+∞ ou -∞), ou diverger sans limite.

Exemple : Suite Arithmétique

Considérons la suite arithmétique définie par u0 = 2 et un+1 = un + 3. Alors u1 = 5, u2 = 8, u3 = 11, etc. Le terme général est un = 2 + 3n.

Exemple : Suite Géométrique

Considérons la suite géométrique définie par u0 = 1 et un+1 = 2un. Alors u1 = 2, u2 = 4, u3 = 8, etc. Le terme général est un = 2n.

Ce qu'il faut retenir

  • Une suite numérique est une fonction définie sur les entiers naturels.
  • Une suite peut être définie explicitement (un = f(n)) ou par récurrence (un+1 = f(un)).
  • Une suite arithmétique a une raison constante (un+1 = un + r).
  • Une suite géométrique a un rapport constant (un+1 = q * un).
  • La convergence d'une suite signifie que ses termes se rapprochent d'une limite finie.

← Stratégies Efficaces pour Réussir l'Épreuve de Mathématiques au Baccalauréat Suites Numériques : Exercices Corrigés pour le Bac →

FAQ

  • Comment déterminer si une suite est arithmétique ou géométrique ?

    Calculez la différence entre les termes consécutifs (un+1 - un). Si cette différence est constante, la suite est arithmétique. Calculez le rapport entre les termes consécutifs (un+1 / un). Si ce rapport est constant, la suite est géométrique.
  • Qu'est-ce qu'une suite divergente ?

    Une suite divergente est une suite qui ne converge pas vers une limite finie. Elle peut diverger vers l'infini (+∞ ou -∞), ou osciller sans s'approcher d'une valeur particulière.